Frequency Response Estimation Basics
Frequency response describes the steady-state response of a system to
sinusoidal inputs. Simulink®
Control Design™ lets you estimate the frequency response of a model or perform online estimation
of a physical plant. The result is a frequency response model, stored as an
frd model object. Applications of frequency response models
include:
Validate exact linearization results. Frequency response estimation uses a different algorithm to compute a linear model approximation and serves as an independent test of exact linearization.
Analyze linear model dynamics or design a controller for the plant represented by the estimated frequency response.
Estimate a parametric model using System Identification Toolbox™ software.
Frequency Response Models
Consider applying a sinusoidal input of frequency ω to a linear system:
The result is an output that is also a sinusoid with the same frequency, but with a different amplitude and phase θ:
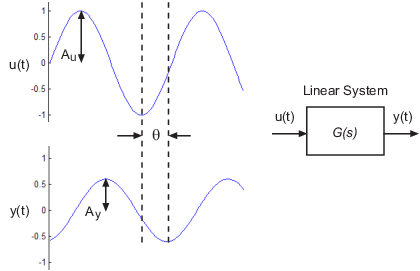
The frequency response for a stable system describes the amplitude change and phase shift as a function of frequency. If Y(s) and U(s) are the Laplace transforms of y(t) and u(t), respectively, then G(s) is:
where
The frd model that you get from frequency response estimation
contains G(s) evaluated at particular frequencies.
Although your Simulink is usually nonlinear, you typically perform estimation at a steady-state
operating point. If the applied perturbation is small, the resulting
frd model is an approximation of the linearized response at that
nominal operating point.
Offline and Online Estimation
Simulink Control Design lets you:
Estimate the frequency response of a system modeled in Simulink, without modifying the model. This approach is sometimes called offline frequency response estimation.
Estimate the frequency response of a physical plant during real-time operation. This approach is called online frequency response estimation.
The following table summarizes some of the differences between offline and online estimation and the tools you use to perform them.
| Goal | Tool | More Information |
|---|---|---|
| Estimate frequency response of a system modeled in Simulink without modifying the model |
| |
| Deploy frequency response estimation algorithm for real-time estimation of a physical plant | Frequency Response Estimator block | Deploy Frequency Response Estimation Algorithm for Real-Time Use |
| Perform online estimation of a plant modeled in Simulink, such as to validate estimation parameters before deployment | Frequency Response Estimator block | Online Estimation Using Plant Modeled in Simulink |
Basic Estimation Workflow
For offline estimation, the basic frequency response estimation workflow includes the following steps:
Specify the portion of the model you want to estimate. You do so by configuring linearization analysis points that specify the inputs and outputs for estimation.
Specify an operating point for estimation. Generally, you perform estimation at a steady-state operating point. You can find such an operating point by trimming the model.
Create an input signal for estimation. The software injects this signal at the input you specify and measures the response at the output.
Perform the estimation and examine the results.
For examples illustrating this workflow, see:
For information about the online estimation workflow, see Online Frequency Response Estimation Basics.
Model Requirements
You can estimate the frequency response of one or more blocks in a stable Simulink model at steady state.
Your model can contain any Simulink blocks, including blocks with event-based dynamics. Examples of blocks with event-based dynamics include Stateflow® charts and triggered subsystems.
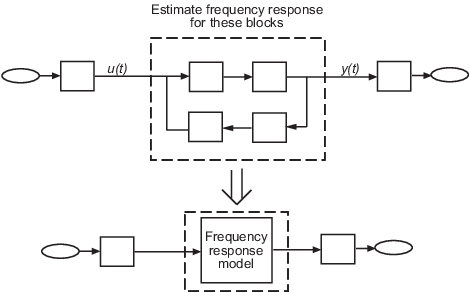
Disable the following types of blocks before estimation:
Blocks that simulate random disturbances (noise). For alternatives ways to model systems with noise, see Estimate Frequency Response Models with Noise Using Signal Processing Toolbox.
Source blocks that generate time-varying outputs that interfere with the estimation. See Effects of Time-Varying Source Blocks on Frequency Response Estimation.
See Also
frestimate | Model Linearizer | Frequency Response
Estimator
Related Topics
- Estimate Frequency Response Using Model Linearizer
- Estimate Frequency Response at the Command Line
- Estimation Input Signals
- Validate Linearization In Frequency Domain Using Model Linearizer
- Estimate Frequency Response Models with Noise Using System Identification Toolbox
- Online Frequency Response Estimation Basics
