makedist
Create probability distribution object
Description
pd = makedist(distname)distname,
using the default parameter values.
Use makedist to specify uniform, normal,
multinomial, piecewise linear, or triangular distribution objects.
If you have Statistics and Machine Learning Toolbox™ software, you can use makedist to
create objects for other distributions, such as the Gamma or Weibull
distributions. For more information, see makedist (Statistics and Machine Learning Toolbox).
To truncate the probability distribution to a specified interval, use truncate (Statistics and Machine Learning Toolbox).
pd = makedist(distname,Name,Value)
list = makedistlist containing a list of the probability
distributions that makedist can create.
Examples
Create Normal Distribution Object
Create a normal distribution object using default parameter values.
pd = makedist('Normal')pd =
NormalDistribution
Normal distribution
mu = 0
sigma = 1
Specify Parameters for a Normal Distribution Object
Create a normal distribution object with a mean value of mu = 75, and a standard deviation of sigma = 10.
pd = makedist('Normal','mu',75,'sigma',10);
Specify Piecewise Linear Distribution Object
Create a piecewise linear distribution object for a distribution with values from 6 to 10, where values from 6 to 8 are four times more likely than values from 8 to 10.
pd = makedist('PieceWiselinear','x',[6 8 10],'Fx',[0 0.8 1]);
You specify the cumulative distribution function Fx as [0 0.8 1] because the difference between 0.8 and 0 is four times the difference between 1 and 0.8. As a result, the generated distribution has four times more values between 6 to 8 than between 8 to 10.
The plot shows the specified cumulative distribution function (CDF) and the corresponding probability distribution function (PDF).
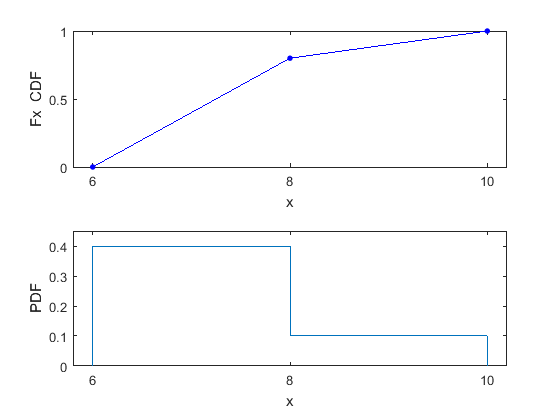
The piecewise linear CDF corresponds to a piecewise constant PDF.
Input Arguments
distname — Distribution name
'Uniform' | 'Normal' | 'Multinomial' | 'PiecewiseLinear' | 'Triangular'
Distribution name, specified as one of the following values:
| Distribution Name | Description |
|---|---|
'Uniform' | Uniform distribution — You specify the lower and upper bounds of the distribution. |
'Normal' | Normal distribution — You specify the mean and standard deviation of the distribution. |
'Multinomial' | Multinomial distribution — In a multinomial distribution, the outcome is one
of 1, 2, ..., k. You specify the
probability of each outcome, [p1,p2,...,
pk]. The probabilities should sum to 1. |
'PiecewiseLinear' |
Piecewise Linear distribution — Use this distribution to make a custom
distribution by specifying a piecewise linear cumulative distribution function (CDF).
You specify the vector of values, For an example, see Specify Piecewise Linear Distribution Object. |
'Triangular' | Triangular distribution — You specify the lower limit, peak location, and upper limit of the distribution. |
For information about these distributions, see the Probability Distributions (Statistics and Machine Learning Toolbox) category.
Note
If you have Statistics and Machine Learning Toolbox software, you can use makedist to
create objects for other distributions, such as the Gamma or Weibull
distributions. For more information, see makedist (Statistics and Machine Learning Toolbox).
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: makedist('Normal','mu',10) specifies
a normal distribution with parameter mu equal to
10, and parameter sigma equal to the default value
of 1.
Probabilities — Outcome probabilities
[0.500 0.500] (default) | vector of scalar values in the range [0,1]
Outcome probabilities for a multinomial distribution, specified as a vector of
scalar values in the range [0,1]. The probabilities sum to 1 and correspond to
outcomes [1, 2, ..., k], where k is the number of elements in the
probabilities vector. This argument is valid only when distname
is 'Multinomial'.
Example: 'Probabilities',[0.1 0.2 0.5 0.2] gives the
probabilities that the outcome is 1, 2, 3, or 4, respectively.
Data Types: single | double
mu — Mean
0 (default) | scalar value
Mean of a normal distribution, specified as a scalar value. This argument is valid
only when distname is 'Normal'.
Example: 'mu',2
Data Types: single | double
sigma — Standard deviation
1 (default) | nonnegative scalar value
Standard deviation of a normal distribution, specified as a nonnegative scalar
value. This argument is valid only when distname is
'Normal'.
Example: 'sigma',2
Data Types: single | double
x — Data values
1 (default) | monotonically increasing vector of scalar values
Data values at which the cumulative distribution function (cdf) changes slope for
a piecewise linear distribution, specified as a monotonically increasing vector of
scalar values. This argument is valid only when distname is
'PiecewiseLinear'.
Example: 'x',[1 2 3]
Data Types: single | double
Fx — cdf value at each value in x
1 (default) | monotonically increasing vector of scalar values that start at 0 and end at
1
A — Lower limit
0 (default) | scalar value
Lower limit for a triangular distribution, specified as a scalar value. This
argument is valid only when distname is
'Triangular'.
Example: 'A',-2
Data Types: single | double
B — Peak location
0.5 (default) | scalar value greater than or equal to A
Peak location for a triangular distribution, specified as a scalar value greater
than or equal to A. This argument is valid only when
distname is 'Triangular'.
Example: 'B',1
Data Types: single | double
C — Upper limit
1 (default) | scalar value greater than or equal to B
Upper limit for a triangular distribution, specified as a scalar value greater
than or equal to B. This argument is valid only when
distname is 'Triangular'.
Example: 'C',5
Data Types: single | double
Lower — Lower limit
0 (default) | scalar value
Lower limit for a uniform distribution, specified as a scalar value. This argument
is valid only when distname is
'Uniform'.
Example: 'Lower',-4
Data Types: single | double
Upper — Upper limit
1 (default) | scalar value greater than Lower
Upper limit for a uniform distribution, specified as a scalar value greater than
Lower. This argument is valid only when
distname is 'Uniform'.
Example: 'Upper',2
Data Types: single | double
Output Arguments
pd — Probability distribution
probability distribution object
Probability distribution, returned as a probability distribution
object of the type specified by distname.
list — List of probability distributions
cell array of character vectors
List of probability distributions that makedist can
create, returned as a cell array of character vectors.
Version History
Introduced in R2014a
See Also
sdo.ParameterSpace | truncate (Statistics and Machine Learning Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)