Compare Grouped Data Using Box Plots
This example shows how to compare two groups of data by creating a notched box plot. Notches display the variability of the median between samples. The width of a notch is computed so that boxes whose notches do not overlap have different medians at the 5% significance level. The significance level is based on a normal distribution assumption, but comparisons of medians are reasonably robust for other distributions. Comparing box plot medians is like a visual hypothesis test, analogous to the t test used for means. For more information on the different features of a box plot, see Box Plot.
Load the fisheriris data set. The data set contains length and width measurements from the sepals and petals of three species of iris flowers. Store the sepal width data for the setosa irises as s1, and the sepal width data for the versicolor irises as s2.
load fisheriris
s1 = meas(1:50,2);
s2 = meas(51:100,2);Create a notched box plot using the sample data, and label each box with the name of the iris species it represents.
boxplot([s1 s2],'Notch','on', ... 'Labels',{'setosa','versicolor'})
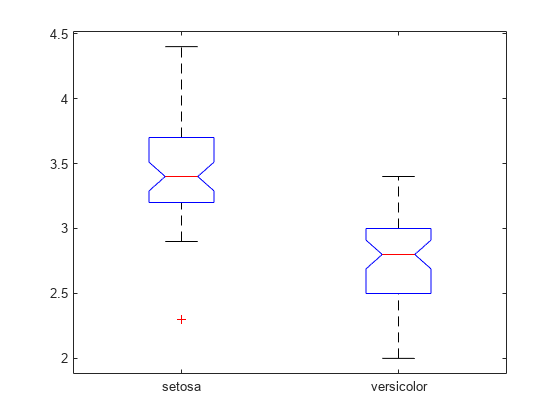
The notches of the two boxes do not overlap, which indicates that the median sepal widths of the setosa and versicolor irises are significantly different at the 5% significance level. Neither the red median line in the setosa box nor the red median line in the versicolor box appears to be centered inside its box, which indicates that each sample is slightly skewed. Additionally, the setosa data contains one outlier value, while the versicolor data does not contain any outliers.
Instead of using the boxplot function, you can use the boxchart MATLAB® function to create box plots. Recreate the previous plot by using the boxchart function rather than boxplot.
speciesName = categorical(species(1:100)); sepalWidth = meas(1:100,2); b = boxchart(speciesName,sepalWidth,'Notch','on');
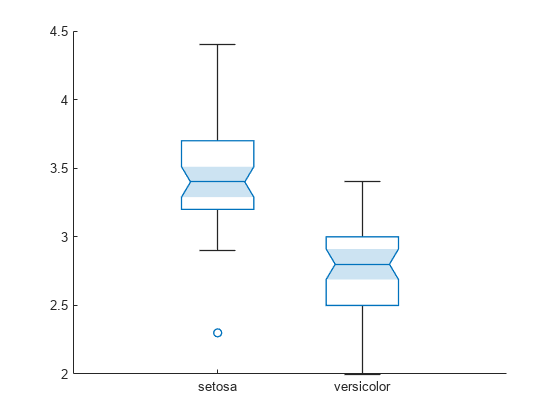
Each notch created by boxchart is a tapered, shaded region around the median line. The shading helps to better identify the notches.
One advantage of using boxchart is that the function creates a BoxChart object, whose properties you can change easily by using dot notation. For example, you can alter the style of the whiskers by specifying the WhiskerLineStyle property of the object b.
b.WhiskerLineStyle = '--';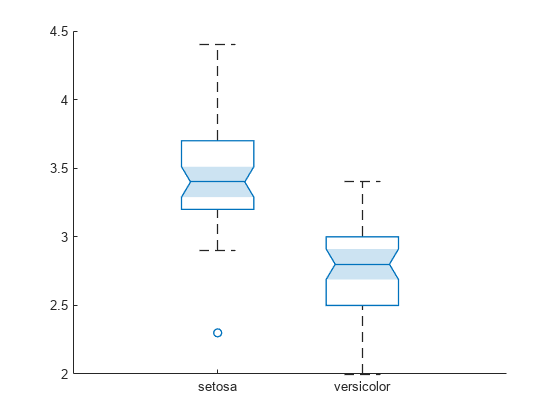
For more information on the advantages of using boxchart, see Alternative Functionality.
See Also
boxplot | iqr | median | boxchart
