resubLoss
Resubstitution classification loss
Description
L = resubLoss(Mdl)Mdl using the training data stored in Mdl.X and
the corresponding class labels stored in Mdl.Y.
The interpretation of L depends on the loss function
('LossFun') and weighting scheme (Mdl.W). In
general, better classifiers yield smaller classification loss values. The default
'LossFun' value varies depending on the model object
Mdl.
L = resubLoss(Mdl,Name,Value)'LossFun','binodeviance' sets the loss function to the binomial
deviance function.
Examples
Determine Resubstitution Loss of Naive Bayes Classifier
Determine the in-sample classification error (resubstitution loss) of a naive Bayes classifier. In general, a smaller loss indicates a better classifier.
Load the fisheriris data set. Create X as a numeric matrix that contains four measurements for 150 irises. Create Y as a cell array of character vectors that contains the corresponding iris species.
load fisheriris
X = meas;
Y = species;Train a naive Bayes classifier using the predictors X and class labels Y. A recommended practice is to specify the class names. fitcnb assumes that each predictor is conditionally and normally distributed.
Mdl = fitcnb(X,Y,'ClassNames',{'setosa','versicolor','virginica'})
Mdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
DistributionNames: {'normal' 'normal' 'normal' 'normal'}
DistributionParameters: {3x4 cell}
Mdl is a trained ClassificationNaiveBayes classifier.
Estimate the in-sample classification error.
L = resubLoss(Mdl)
L = 0.0400
The naive Bayes classifier misclassifies 4% of the training observations.
Determine Resubstitution Hinge Loss of SVM Classifier
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').
load ionosphereTrain a support vector machine (SVM) classifier. Standardize the data and specify that 'g' is the positive class.
SVMModel = fitcsvm(X,Y,'ClassNames',{'b','g'},'Standardize',true);
SVMModel is a trained ClassificationSVM classifier.
Estimate the in-sample hinge loss.
L = resubLoss(SVMModel,'LossFun','hinge')
L = 0.1603
The hinge loss is 0.1603. Classifiers with hinge losses close to 0 are preferred.
Compare GAMs by Examining Classification Loss
Train a generalized additive model (GAM) that contains both linear and interaction terms for predictors, and estimate the classification loss with and without interaction terms. Specify whether to include interaction terms when estimating the classification loss for training and test data.
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').
load ionospherePartition the data set into two sets: one containing training data, and the other containing new, unobserved test data. Reserve 50 observations for the new test data set.
rng('default') % For reproducibility n = size(X,1); newInds = randsample(n,50); inds = ~ismember(1:n,newInds); XNew = X(newInds,:); YNew = Y(newInds);
Train a GAM using the predictors X and class labels Y. A recommended practice is to specify the class names. Specify to include the 10 most important interaction terms.
Mdl = fitcgam(X(inds,:),Y(inds),'ClassNames',{'b','g'},'Interactions',10)
Mdl =
ClassificationGAM
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'logit'
Intercept: 2.0026
Interactions: [10x2 double]
NumObservations: 301
Mdl is a ClassificationGAM model object.
Compute the resubstitution classification loss both with and without interaction terms in Mdl. To exclude interaction terms, specify 'IncludeInteractions',false.
resubl = resubLoss(Mdl)
resubl = 0
resubl_nointeraction = resubLoss(Mdl,'IncludeInteractions',false)resubl_nointeraction = 0
Estimate the classification loss both with and without interaction terms in Mdl.
l = loss(Mdl,XNew,YNew)
l = 0.0615
l_nointeraction = loss(Mdl,XNew,YNew,'IncludeInteractions',false)l_nointeraction = 0.0615
Including interaction terms does not change the classification loss for Mdl. The trained model classifies all training samples correctly and misclassifies approximately 6% of the test samples.
Input Arguments
Mdl — Classification machine learning model
full classification model object
Classification machine learning model, specified as a full classification model object, as given in the following table of supported models.
| Model | Classification Model Object |
|---|---|
| Generalized additive model | ClassificationGAM |
| k-nearest neighbor model | ClassificationKNN |
| Naive Bayes model | ClassificationNaiveBayes |
| Neural network model | ClassificationNeuralNetwork |
| Support vector machine for one-class and binary classification | ClassificationSVM |
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: resubLoss(Mdl,'LossFun','logit') estimates the logit
resubstitution loss.
IncludeInteractions — Flag to include interaction terms
true | false
Flag to include interaction terms of the model, specified as true or
false. This argument is valid only for a generalized
additive model (GAM). That is, you can specify this argument only when
Mdl is ClassificationGAM.
The default value is true if Mdl contains interaction
terms. The value must be false if the model does not contain interaction
terms.
Data Types: logical
LossFun — Loss function
'binodeviance' | 'classifcost' | 'classiferror' | 'crossentropy' | 'exponential' | 'hinge' | 'logit' | 'mincost' | 'quadratic' | function handle
Loss function, specified as a built-in loss function name or a function handle.
The default value depends on the model type of Mdl.
The default value is
'classiferror'ifMdlis aClassificationSVMobject.The default value is
'mincost'ifMdlis aClassificationKNN,ClassificationNaiveBayes, orClassificationNeuralNetworkobject.If
Mdlis aClassificationGAMobject, the default value is'mincost'if theScoreTransformproperty of the input model object (Mdl.ScoreTransform'logit'; otherwise, the default value is'classiferror'.
'classiferror' and 'mincost' are equivalent
when you use the default cost matrix. See Classification Loss for more
information.
This table lists the available loss functions. Specify one using its corresponding character vector or string scalar.
Value Description 'binodeviance'Binomial deviance 'classifcost'Observed misclassification cost 'classiferror'Misclassified rate in decimal 'crossentropy'Cross-entropy loss (for neural networks only) 'exponential'Exponential loss 'hinge'Hinge loss 'logit'Logistic loss 'mincost'Minimal expected misclassification cost (for classification scores that are posterior probabilities) 'quadratic'Quadratic loss To specify a custom loss function, use function handle notation. The function must have this form:
lossvalue =lossfun(C,S,W,Cost)The output argument
lossvalueis a scalar.You specify the function name (
lossfun).Cis ann-by-Klogical matrix with rows indicating the class to which the corresponding observation belongs.nis the number of observations inTblorX, andKis the number of distinct classes (numel(Mdl.ClassNames)). The column order corresponds to the class order inMdl.ClassNames. CreateCby settingC(p,q) = 1, if observationpis in classq, for each row. Set all other elements of rowpto0.Sis ann-by-Knumeric matrix of classification scores. The column order corresponds to the class order inMdl.ClassNames.Sis a matrix of classification scores, similar to the output ofpredict.Wis ann-by-1 numeric vector of observation weights.Costis aK-by-Knumeric matrix of misclassification costs. For example,Cost = ones(K) – eye(K)specifies a cost of0for correct classification and1for misclassification.
Example: 'LossFun','binodeviance'
Data Types: char | string | function_handle
More About
Classification Loss
Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.
Consider the following scenario.
L is the weighted average classification loss.
n is the sample size.
For binary classification:
yj is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the
ClassNamesproperty), respectively.f(Xj) is the positive-class classification score for observation (row) j of the predictor data X.
mj = yjf(Xj) is the classification score for classifying observation j into the class corresponding to yj. Positive values of mj indicate correct classification and do not contribute much to the average loss. Negative values of mj indicate incorrect classification and contribute significantly to the average loss.
For algorithms that support multiclass classification (that is, K ≥ 3):
yj* is a vector of K – 1 zeros, with 1 in the position corresponding to the true, observed class yj. For example, if the true class of the second observation is the third class and K = 4, then y2* = [
0 0 1 0]′. The order of the classes corresponds to the order in theClassNamesproperty of the input model.f(Xj) is the length K vector of class scores for observation j of the predictor data X. The order of the scores corresponds to the order of the classes in the
ClassNamesproperty of the input model.mj = yj*′f(Xj). Therefore, mj is the scalar classification score that the model predicts for the true, observed class.
The weight for observation j is wj. The software normalizes the observation weights so that they sum to the corresponding prior class probability stored in the
Priorproperty. Therefore,
Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.
| Loss Function | Value of LossFun | Equation |
|---|---|---|
| Binomial deviance | "binodeviance" | |
| Observed misclassification cost | "classifcost" | where is the class label corresponding to the class with the maximal score, and is the user-specified cost of classifying an observation into class when its true class is yj. |
| Misclassified rate in decimal | "classiferror" | where I{·} is the indicator function. |
| Cross-entropy loss | "crossentropy" |
The weighted cross-entropy loss is where the weights are normalized to sum to n instead of 1. |
| Exponential loss | "exponential" | |
| Hinge loss | "hinge" | |
| Logit loss | "logit" | |
| Minimal expected misclassification cost | "mincost" |
The software computes the weighted minimal expected classification cost using this procedure for observations j = 1,...,n.
The weighted average of the minimal expected misclassification cost loss is |
| Quadratic loss | "quadratic" |
If you use the default cost matrix (whose element value is 0 for correct classification
and 1 for incorrect classification), then the loss values for
"classifcost", "classiferror", and
"mincost" are identical. For a model with a nondefault cost matrix,
the "classifcost" loss is equivalent to the "mincost"
loss most of the time. These losses can be different if prediction into the class with
maximal posterior probability is different from prediction into the class with minimal
expected cost. Note that "mincost" is appropriate only if classification
scores are posterior probabilities.
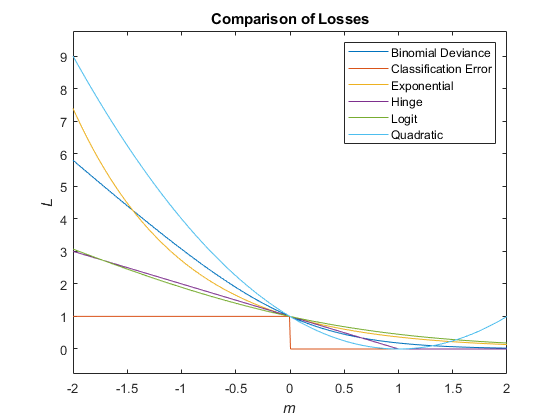
This figure compares the loss functions (except "classifcost",
"crossentropy", and "mincost") over the score
m for one observation. Some functions are normalized to pass through
the point (0,1).
Algorithms
resubLoss computes the classification loss according to the
corresponding loss function of the object (Mdl). For
a model-specific description, see the loss function reference pages in
the following table.
| Model | Classification Model Object (Mdl) | loss Object Function |
|---|---|---|
| Generalized additive model | ClassificationGAM | loss |
| k-nearest neighbor model | ClassificationKNN | loss |
| Naive Bayes model | ClassificationNaiveBayes | loss |
| Neural network model | ClassificationNeuralNetwork | loss |
| Support vector machine for one-class and binary classification | ClassificationSVM | loss |
Extended Capabilities
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
This function fully supports GPU arrays for a trained classification model specified as a
ClassificationKNNorClassificationSVMobject.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2012aR2023b: Observations with missing predictor values are used in resubstitution and cross-validation computations
Starting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.
In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.
R2022a: resubLoss returns a different value for a ClassificationSVM model with a nondefault cost matrix
If you specify a nondefault cost matrix when you train the input model object for an SVM model, the resubLoss function returns a different value compared to previous releases.
The resubLoss function uses the
observation weights stored in the W property. Also, the function uses the
cost matrix stored in the Cost property if you specify the
LossFun name-value argument as "classifcost" or
"mincost". The way the function uses the W and
Cost property values has not changed. However, the property values stored in the input model object have changed for
a ClassificationSVM model object with a nondefault cost matrix, so the
function can return a different value.
For details about the property value change, see Cost property stores the user-specified cost matrix.
If you want the software to handle the cost matrix, prior
probabilities, and observation weights in the same way as in previous releases, adjust the prior
probabilities and observation weights for the nondefault cost matrix, as described in Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix. Then, when you train a
classification model, specify the adjusted prior probabilities and observation weights by using
the Prior and Weights name-value arguments, respectively,
and use the default cost matrix.
R2022a: Default LossFun value has changed for ClassificationGAM and
ClassificationNeuralNetwork
Starting in R2022a, the default value of the LossFun name-value
argument has changed for both a generalized additive model (GAM) and a neural network model,
so that the resubLoss function uses the "mincost"
option (minimal expected misclassification cost) as the default when a classification object
uses posterior probabilities for classification scores.
If the input model object
Mdlis aClassificationGAMobject, the default value is"mincost"if theScoreTransformproperty ofMdl(Mdl.ScoreTransform'logit'; otherwise, the default value is"classiferror".If
Mdlis aClassificationNeuralNetworkobject, the default value is"mincost".
In previous releases, the default value was
"classiferror".
You do not need to make any changes to your code if you use the default cost matrix (whose element value is 0 for correct classification and 1 for incorrect classification). The "mincost" option is equivalent to the "classiferror" option for the default cost matrix.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)