resubLoss
Resubstitution classification loss for classification tree model
Description
L = resubLoss(tree)L by resubstitution for the trained classification tree model
tree using the training data stored in tree.X and
the corresponding true class labels stored in tree.Y. By default,
resubLoss uses the loss computed for the data used by fitctree to create tree.
The classification loss (L) is a resubstitution quality measure. Its
interpretation depends on the loss function (LossFun), but in general,
better classifiers yield smaller classification loss values. The default
LossFun value is "mincost" (minimal expected
misclassification cost).
L = resubLoss(
specifies additional options using one or more name-value arguments. For example, you can
specify the loss function, pruning level, and the tree size that
tree,Name=Value)resubLoss uses to calculate the classification loss.
[
also returns the standard errors of the classification errors, the number of leaf nodes in
the trees of the pruning sequence, and the best pruning level as defined in the L,SE,Nleaf,BestLevel] = resubLoss(___)TreeSize name-value argument. By default, BestLevel is
the pruning level that gives loss within one standard deviation of the minimal loss.
Examples
Compute the In-Sample Classification Error
Compute the resubstitution classification error for the ionosphere data.
load ionosphere
tree = fitctree(X,Y);
L = resubLoss(tree)L = 0.0114
Examine the Classification Error for Each Subtree
Unpruned decision trees tend to overfit. One way to balance model complexity and out-of-sample performance is to prune a tree (or restrict its growth) so that in-sample and out-of-sample performance are satisfactory.
Load Fisher's iris data set. Partition the data into training (50%) and validation (50%) sets.
load fisheriris n = size(meas,1); rng(1) % For reproducibility idxTrn = false(n,1); idxTrn(randsample(n,round(0.5*n))) = true; % Training set logical indices idxVal = idxTrn == false; % Validation set logical indices
Grow a classification tree using the training set.
Mdl = fitctree(meas(idxTrn,:),species(idxTrn));
View the classification tree.
view(Mdl,'Mode','graph');
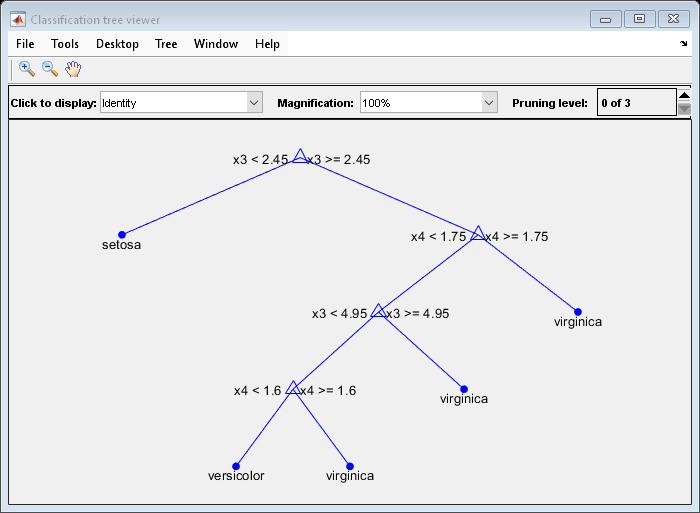
The classification tree has four pruning levels. Level 0 is the full, unpruned tree (as displayed). Level 3 is just the root node (i.e., no splits).
Examine the training sample classification error for each subtree (or pruning level) excluding the highest level.
m = max(Mdl.PruneList) - 1;
trnLoss = resubLoss(Mdl,'Subtrees',0:m)trnLoss = 3×1
0.0267
0.0533
0.3067
The full, unpruned tree misclassifies about 2.7% of the training observations.
The tree pruned to level 1 misclassifies about 5.3% of the training observations.
The tree pruned to level 2 (i.e., a stump) misclassifies about 30.6% of the training observations.
Examine the validation sample classification error at each level excluding the highest level.
valLoss = loss(Mdl,meas(idxVal,:),species(idxVal),'Subtrees',0:m)valLoss = 3×1
0.0369
0.0237
0.3067
The full, unpruned tree misclassifies about 3.7% of the validation observations.
The tree pruned to level 1 misclassifies about 2.4% of the validation observations.
The tree pruned to level 2 (i.e., a stump) misclassifies about 30.7% of the validation observations.
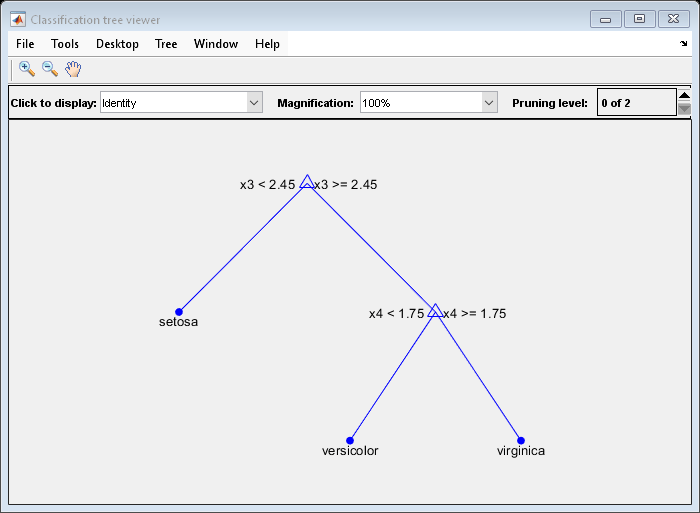
To balance model complexity and out-of-sample performance, consider pruning Mdl to level 1.
pruneMdl = prune(Mdl,'Level',1); view(pruneMdl,'Mode','graph')
Input Arguments
tree — Classification tree model
ClassificationTree model object
Classification tree model, specified as a ClassificationTree model object trained with fitctree.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: L = resubLoss(tree,Subtrees="all") specifies to use all
subtrees when computing the resubstitution classification loss for
tree.
LossFun — Loss function
"mincost" (default) | "binodeviance" | "classifcost" | "classiferror" | "exponential" | "hinge" | "logit" | "quadratic" | function handle
Loss function, specified as a built-in loss function name or a function handle.
The following table describes the values for the built-in loss functions.
| Value | Description |
|---|---|
"binodeviance" | Binomial deviance |
"classifcost" | Observed misclassification cost |
"classiferror" | Misclassified rate in decimal |
"exponential" | Exponential loss |
"hinge" | Hinge loss |
"logit" | Logistic loss |
"mincost" | Minimal expected misclassification cost (for classification scores that are posterior probabilities) |
"quadratic" | Quadratic loss |
"mincost" is appropriate for classification scores
that are posterior probabilities. Classification trees return posterior probabilities
as classification scores by default (see predict).
Specify your own function using function handle notation. Suppose that
n is the number of observations in X, and
K is the number of distinct classes
(numel(tree.ClassNames)). Your function must have the signature
lossvalue = lossfun(C,S,W,Cost)The output argument
lossvalueis a scalar.You specify the function name (
lossfun).Cis an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs. The column order corresponds to the class order intree.ClassNames.Create
Cby settingC(p,q) = 1, if observationpis in classq, for each row. Set all other elements of rowpto0.Sis an n-by-K numeric matrix of classification scores. The column order corresponds to the class order intree.ClassNames.Sis a matrix of classification scores, similar to the output ofpredict.Wis an n-by-1 numeric vector of observation weights. If you passW, the software normalizes the weights to sum to1.Costis a K-by-K numeric matrix of misclassification costs. For example,Cost = ones(K) - eye(K)specifies a cost of0for correct classification and1for misclassification.
For more details on loss functions, see Classification Loss.
Example: LossFun="binodeviance"
Example: LossFun=@lossfun
Data Types: char | string | function_handle
Subtrees — Pruning level
0 (default) | vector of nonnegative integers | "all"
Pruning level, specified as a vector of nonnegative integers in ascending order or
"all".
If you specify a vector, then all elements must be at least 0 and
at most max(tree.PruneList). 0 indicates the full,
unpruned tree, and max(tree.PruneList) indicates the completely
pruned tree (that is, just the root node).
If you specify "all", then resubLoss
operates on all subtrees (in other words, the entire pruning sequence). This
specification is equivalent to using 0:max(tree.PruneList).
resubLoss prunes tree to each level
specified by Subtrees, and then estimates the corresponding output
arguments. The size of Subtrees determines the size of some output
arguments.
For the function to invoke Subtrees, the properties
PruneList and PruneAlpha of
tree must be nonempty. In other words, grow
tree by setting Prune="on" when you use
fitctree, or by pruning tree using prune.
Example: Subtrees="all"
Data Types: single | double | char | string
TreeSize — Tree size
"se" (default) | "min"
Tree size, specified as one of these values:
"se"—resubLossreturns the best pruning level (BestLevel), which corresponds to the highest pruning level with the loss within one standard deviation of the minimum (L+se, whereLandserelate to the smallest value inSubtrees)."min"—resubLossreturns the best pruning level, which corresponds to the element ofSubtreeswith the smallest loss. This element is usually the smallest element ofSubtrees.
Example: TreeSize="min"
Data Types: char | string
Output Arguments
L — Classification loss
numeric vector
Classification
loss, returned as a vector of scalar values that has the same length as
Subtrees. The meaning of the error depends on the loss function
(LossFun).
SE — Standard error of loss
numeric vector
Standard error of loss, returned as a numeric vector of the same length as
Subtrees.
Nleaf — Number of leaf nodes
vector of integer values
Number of leaf nodes in the pruned subtrees, returned as a vector of integer values
that has the same length as Subtrees. Leaf nodes are terminal
nodes, which give responses, not splits.
BestLevel — Best pruning level
numeric scalar
Best pruning level, returned as a numeric scalar whose value depends on
TreeSize:
When
TreeSizeis"se", thelossfunction returns the highest pruning level whose loss is within one standard deviation of the minimum (L+se, whereLandserelate to the smallest value inSubtrees).When
TreeSizeis"min", thelossfunction returns the element ofSubtreeswith the smallest loss, usually the smallest element ofSubtrees.
More About
Classification Loss
Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.
Consider the following scenario.
L is the weighted average classification loss.
n is the sample size.
For binary classification:
yj is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the
ClassNamesproperty), respectively.f(Xj) is the positive-class classification score for observation (row) j of the predictor data X.
mj = yjf(Xj) is the classification score for classifying observation j into the class corresponding to yj. Positive values of mj indicate correct classification and do not contribute much to the average loss. Negative values of mj indicate incorrect classification and contribute significantly to the average loss.
For algorithms that support multiclass classification (that is, K ≥ 3):
yj* is a vector of K – 1 zeros, with 1 in the position corresponding to the true, observed class yj. For example, if the true class of the second observation is the third class and K = 4, then y2* = [
0 0 1 0]′. The order of the classes corresponds to the order in theClassNamesproperty of the input model.f(Xj) is the length K vector of class scores for observation j of the predictor data X. The order of the scores corresponds to the order of the classes in the
ClassNamesproperty of the input model.mj = yj*′f(Xj). Therefore, mj is the scalar classification score that the model predicts for the true, observed class.
The weight for observation j is wj. The software normalizes the observation weights so that they sum to the corresponding prior class probability stored in the
Priorproperty. Therefore,
Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.
| Loss Function | Value of LossFun | Equation |
|---|---|---|
| Binomial deviance | "binodeviance" | |
| Observed misclassification cost | "classifcost" | where is the class label corresponding to the class with the maximal score, and is the user-specified cost of classifying an observation into class when its true class is yj. |
| Misclassified rate in decimal | "classiferror" | where I{·} is the indicator function. |
| Cross-entropy loss | "crossentropy" |
The weighted cross-entropy loss is where the weights are normalized to sum to n instead of 1. |
| Exponential loss | "exponential" | |
| Hinge loss | "hinge" | |
| Logit loss | "logit" | |
| Minimal expected misclassification cost | "mincost" |
The software computes the weighted minimal expected classification cost using this procedure for observations j = 1,...,n.
The weighted average of the minimal expected misclassification cost loss is |
| Quadratic loss | "quadratic" |
If you use the default cost matrix (whose element value is 0 for correct classification
and 1 for incorrect classification), then the loss values for
"classifcost", "classiferror", and
"mincost" are identical. For a model with a nondefault cost matrix,
the "classifcost" loss is equivalent to the "mincost"
loss most of the time. These losses can be different if prediction into the class with
maximal posterior probability is different from prediction into the class with minimal
expected cost. Note that "mincost" is appropriate only if classification
scores are posterior probabilities.
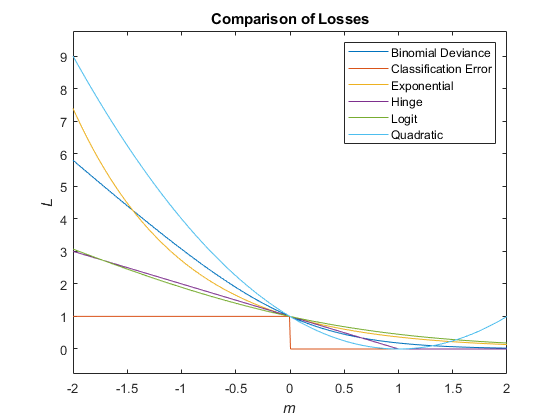
This figure compares the loss functions (except "classifcost",
"crossentropy", and "mincost") over the score
m for one observation. Some functions are normalized to pass through
the point (0,1).
True Misclassification Cost
The true misclassification cost is the cost of classifying an observation into an incorrect class.
You can set the true misclassification cost per class by using the Cost
name-value argument when you create the classifier. Cost(i,j) is the cost
of classifying an observation into class j when its true class is
i. By default, Cost(i,j)=1 if
i~=j, and Cost(i,j)=0 if i=j.
In other words, the cost is 0 for correct classification and
1 for incorrect classification.
Expected Misclassification Cost
The expected misclassification cost per observation is an averaged cost of classifying the observation into each class.
Suppose you have Nobs observations that you want to classify with a trained
classifier, and you have K classes. You place the observations
into a matrix X with one observation per row.
The expected cost matrix CE has size
Nobs-by-K. Each row of
CE contains the expected (average) cost of classifying
the observation into each of the K classes.
CE(n,k)
is
where:
K is the number of classes.
is the posterior probability of class i for observation X(n).
is the true misclassification cost of classifying an observation as k when its true class is i.
Extended Capabilities
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2011a
See Also
loss | resubEdge | resubMargin | resubPredict | fitctree | ClassificationTree
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)