cluster
Construct agglomerative clusters from linkages
Syntax
Description
T = cluster(Z,'Cutoff',C)Z.
The input Z is the output of the linkage function for an input data matrix X.
cluster cuts Z into clusters, using
C as a threshold for the inconsistency coefficients (or inconsistent values) of nodes in the tree. The output T
contains cluster assignments of each observation (row of X).
Examples
Define Clusters by Specifying Depth
Perform agglomerative clustering on randomly generated data by evaluating inconsistent values to a depth of four below each node.
Randomly generate the sample data.
rng('default'); % For reproducibility X = [(randn(20,2)*0.75)+1; (randn(20,2)*0.25)-1];
Create a scatter plot of the data.
scatter(X(:,1),X(:,2));
title('Randomly Generated Data');
Create a hierarchical cluster tree using the ward linkage method.
Z = linkage(X,'ward');Create a dendrogram plot of the data.
dendrogram(Z)

The scatter plot and the dendrogram plot seem to show two clusters in the data.
Cluster the data using a threshold of 3 for the inconsistency coefficient and looking to a depth of 4 below each node. Plot the resulting clusters.
T = cluster(Z,'cutoff',3,'Depth',4); gscatter(X(:,1),X(:,2),T)

cluster identifies two clusters in the data.
Cluster Data Using Distance Criterion
Perform agglomerative clustering on the fisheriris data set using 'distance' as the criterion for defining clusters. Visualize the cluster assignments of the data.
Load the fisheriris data set.
load fisheririsVisualize a 2-D scatter plot of the data using species as the grouping variable. Specify marker colors and marker symbols for the three different species.
gscatter(meas(:,1),meas(:,2),species,'rgb','do*') title("Actual Clusters of Fisher's Iris Data")

Create a hierarchical cluster tree using the 'average' method and the 'chebychev' metric.
Z = linkage(meas,'average','chebychev');
Cluster the data using a threshold of 1.5 for the 'distance' criterion.
T = cluster(Z,'cutoff',1.5,'Criterion','distance')
T = 150×1
2
2
2
2
2
2
2
2
2
2
⋮
T contains numbers that correspond to the cluster assignments. Find the number of classes that cluster identifies.
length(unique(T))
ans = 3
cluster identifies three classes for the specified values of cutoff and Criterion.
Visualize a 2-D scatter plot of the clustering results using T as the grouping variable. Specify marker colors and marker symbols for the three different classes.
gscatter(meas(:,1),meas(:,2),T,'rgb','do*') title("Cluster Assignments of Fisher's Iris Data")

Clustering correctly identifies the setosa class (class 2) as belonging to a distinct cluster, but poorly distinguishes between the versicolor and virginica classes (classes 1 and 3, respectively). Note that the scatter plot labels the classes using the numbers contained in T.
Compare Cluster Assignments to Classes
Find a maximum of three clusters in the fisheriris data set and compare cluster assignments of the flowers to their known classification.
Load the sample data.
load fisheririsCreate a hierarchical cluster tree using the 'average' method and the 'chebychev' metric.
Z = linkage(meas,'average','chebychev');
Find a maximum of three clusters in the data.
T = cluster(Z,'maxclust',3);Create a dendrogram plot of Z. To see the three clusters, use 'ColorThreshold' with a cutoff halfway between the third-from-last and second-from-last linkages.
cutoff = median([Z(end-2,3) Z(end-1,3)]);
dendrogram(Z,'ColorThreshold',cutoff)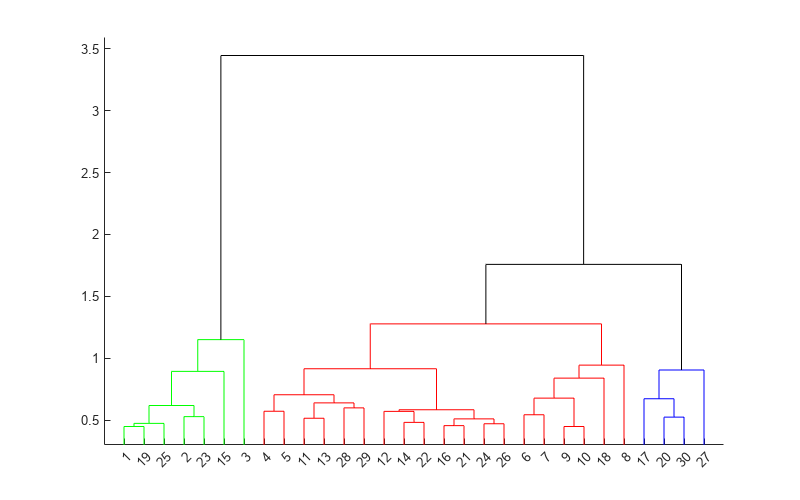
Display the last two rows of Z to see how the three clusters are combined into one. linkage combines the 293rd (blue) cluster with the 297th (red) cluster to form the 298th cluster with a linkage of 1.7583. linkage then combines the 296th (green) cluster with the 298th cluster.
lastTwo = Z(end-1:end,:)
lastTwo = 2×3
293.0000 297.0000 1.7583
296.0000 298.0000 3.4445
See how the cluster assignments correspond to the three species. For example, one of the clusters contains 50 flowers of the second species and 40 flowers of the third species.
crosstab(T,species)
ans = 3×3
0 0 10
0 50 40
50 0 0
Cluster Data and Plot Result
Randomly generate sample data with 20,000 observations.
rng('default') % For reproducibility X = rand(20000,3);
Create a hierarchical cluster tree using the ward linkage method. In this case, the 'SaveMemory' option of the clusterdata function is set to 'on' by default. In general, specify the best value for 'SaveMemory' based on the dimensions of X and the available memory.
Z = linkage(X,'ward');Cluster the data into a maximum of four groups and plot the result.
c = cluster(Z,'Maxclust',4);
scatter3(X(:,1),X(:,2),X(:,3),10,c)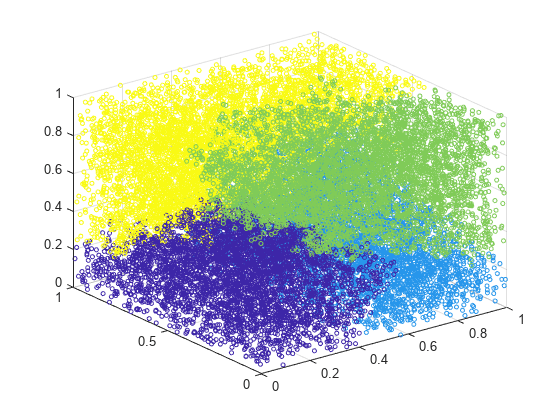
cluster identifies four groups in the data.
Input Arguments
Z — Agglomerative hierarchical cluster tree
numeric matrix
Agglomerative hierarchical cluster tree that is the output of the linkage function, specified as a numeric matrix. For an input data matrix
X with m rows (or observations),
linkage returns an (m – 1)-by-3 matrix Z. For an explanation of how
linkage creates the cluster tree, see Z.
Example: Z = linkage(X), where X is an input
data matrix
Data Types: single | double
C — Threshold for defining clusters
positive scalar | vector of positive scalars
Threshold for defining clusters, specified as a positive scalar or a vector of
positive scalars. cluster uses C as a
threshold for either the heights or the inconsistency coefficients of nodes, depending
on the criterion for defining clusters in a hierarchical cluster tree.
If the criterion for defining clusters is
'distance', thenclustergroups all leaves at or below a node into a cluster, provided that the height of the node is less thanC.If the criterion for defining clusters is
'inconsistent', then theinconsistentvalues of a node and all its subnodes must be less thanCforclusterto group them into a cluster.clusterbegins from the root of the cluster treeZand steps down through the tree until it encounters a node whoseinconsistentvalue is less than the thresholdC, and whose subnodes (or descendants) have inconsistent values less thanC. Thenclustergroups all leaves at or below the node into a cluster (or a singleton if the node itself is a leaf).clusterfollows every branch in the tree until all leaf nodes are in clusters.
Example: cluster(Z,'Cutoff',0.5)
Data Types: single | double
D — Depth for computing inconsistent values
2 (default) | numeric scalar
Depth for computing inconsistent values, specified as a numeric scalar.
cluster evaluates inconsistent values by looking to a depth
D below each node.
Example: cluster(Z,'Cutoff',0.5,'Depth',3)
Data Types: single | double
criterion — Criterion for defining clusters
'inconsistent' (default) | 'distance'
Criterion for defining clusters, specified as 'inconsistent' or
'distance'.
If the criterion for defining clusters is 'distance', then
cluster groups all leaves at or below a node into a cluster (or a
singleton if the node itself is a leaf), provided that the height of the node is less
than C. The height of a node in a tree represents the distance
between the two subnodes that are merged at that node. Specifying
'distance' results in clusters that correspond to a horizontal
slice of the dendrogram plot of
Z.
If the criterion for defining clusters is 'inconsistent', then
cluster groups a node and all its subnodes into a cluster,
provided that the inconsistency coefficients (or inconsistent values) of the node and subnodes are less than
C. Specifying 'inconsistent' is equivalent to
cluster(Z,'Cutoff',C).
Example: cluster(Z,'Cutoff',0.5,'Criterion','distance')
Data Types: char | string
N — Maximum number of clusters
positive integer | vector of positive integers
Maximum number of clusters to form, specified as a positive integer or a vector of
positive integers. cluster constructs a maximum of
N clusters, using 'distance' as the
criterion for defining clusters. The height of each node in the tree represents the
distance between the two subnodes merged at that node. cluster
finds the smallest height at which a horizontal cut through the tree will leave
N or fewer clusters. See Specify Arbitrary Clusters for more details.
Example: cluster(Z,'MaxClust',5)
Data Types: single | double
Output Arguments
T — Cluster assignment
numeric vector | numeric matrix
Cluster assignment, returned as a numeric vector or matrix. For the (m – 1)-by-3 hierarchical cluster tree Z (the output of
linkage given input X),
T contains the cluster assignments of the m
rows (observations) of X.
The size of T depends on the corresponding size of
C or N.
If
Cis a positive scalar, thenTis a vector of length m.If
Nis a positive integer, thenTis a vector of length m.If
Cis a length l vector of positive scalars, thenTis an m-by-l matrix with one column per value inC.If
Nis a length l vector of positive integers, thenTis an m-by-l matrix with one column per value inN.
Alternative Functionality
If you have an input data matrix X, you can use clusterdata to perform agglomerative clustering and return cluster indices for
each observation (row) in X. The clusterdata function
performs all the necessary steps for you, so you do not need to execute the pdist, linkage, and cluster
functions separately.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)