clusterdata
Construct agglomerative clusters from data
Description
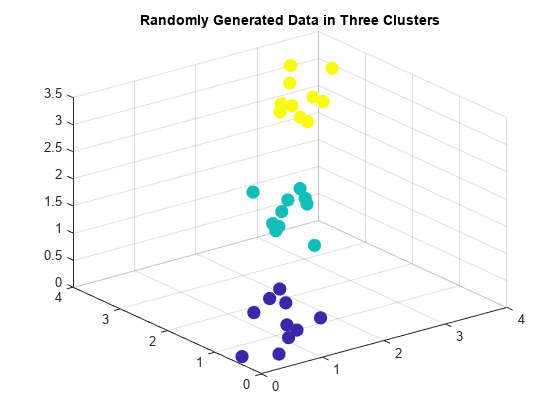
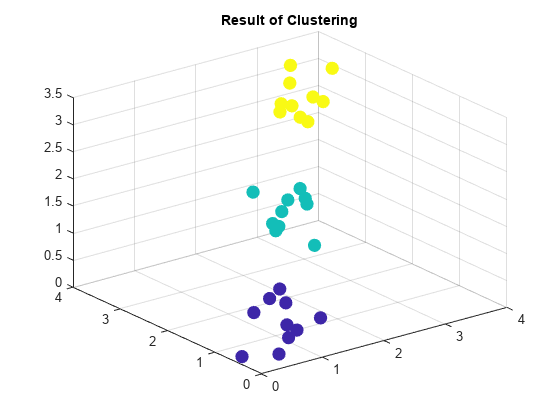
T = clusterdata(X,cutoff)X, given a threshold cutoff for cutting an
agglomerative hierarchical tree that the linkage function generates from X.
clusterdata supports agglomerative clustering and incorporates
the pdist, linkage, and
cluster functions, which you can use
separately for more detailed analysis. See Algorithm Description for more details.
Examples
Input Arguments
Output Arguments
Tips
If
'Linkage'is'centroid'or'median', thenlinkagecan produce a cluster tree that is not monotonic. This result occurs when the distance from the union of two clusters, r and s, to a third cluster is less than the distance between r and s. In this case, in a dendrogram drawn with the default orientation, the path from a leaf to the root node takes some downward steps. To avoid this result, specify another value for'Linkage'. The following image shows a nonmonotonic cluster tree.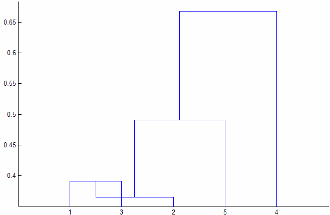
In this case, cluster 1 and cluster 3 are joined into a new cluster, while the distance between this new cluster and cluster 2 is less than the distance between cluster 1 and cluster 3.
Algorithms
If you specify a value c for the cutoff input
argument, then T =
clusterdata(X,c)
Create a vector of the Euclidean distance between pairs of observations in
Xby usingpdist.Y =pdist(X,'euclidean')Create an agglomerative hierarchical cluster tree from
Yby usinglinkagewith the'single'method for computing the shortest distance between clusters.Z =linkage(Y,'single')If
0 <c< 2, useclusterto define clusters fromZwhen inconsistent values are less thanc.T=cluster(Z,'Cutoff',c)If
cis an integer value≥ 2, useclusterto find a maximum ofcclusters fromZ.T= cluster(Z,'MaxClust',c)
Alternative Functionality
If you have a hierarchical cluster tree Z (the output of the linkage function for the input data matrix X), you can use
cluster to perform agglomerative clustering on Z and return
the cluster assignment for each observation (row) in X.
Version History
Introduced before R2006a