ecdf
Empirical cumulative distribution function
Description
[
specifies additional options using one or more name-value arguments. For example,
f,x]
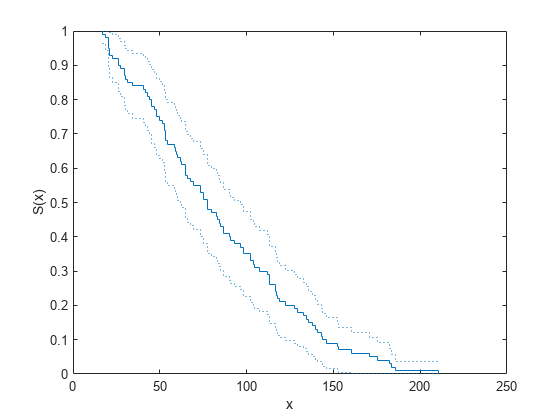
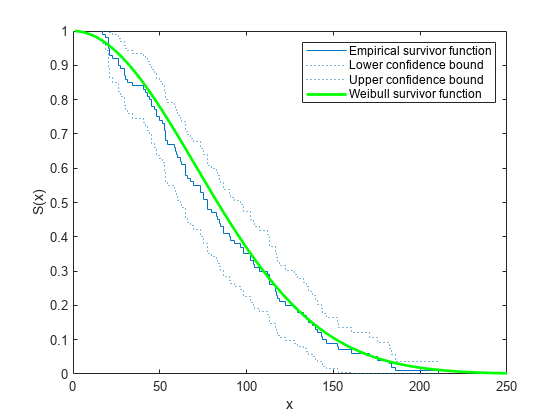
= ecdf(y,Name,Value)'Function','survivor'f as a survivor function.
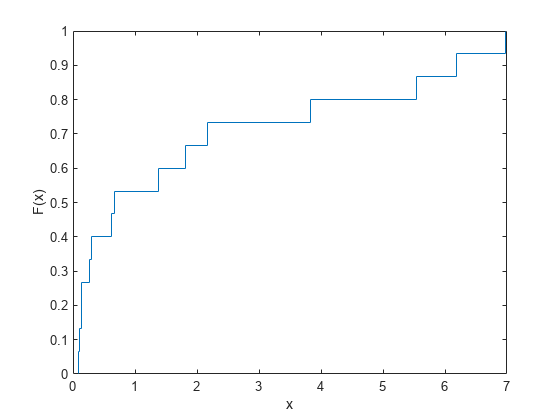
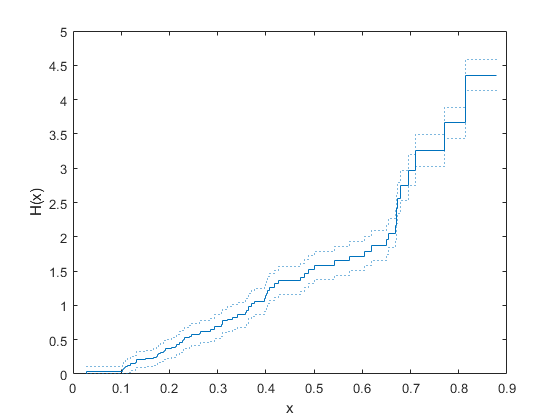
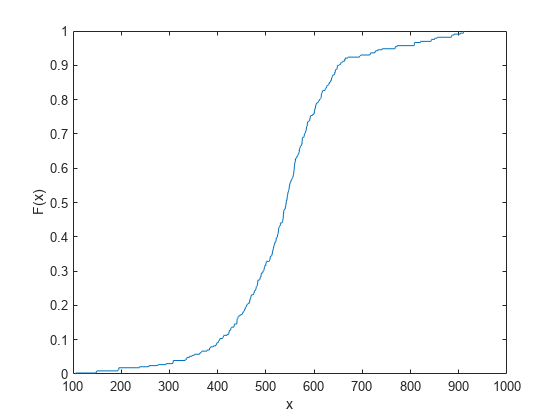
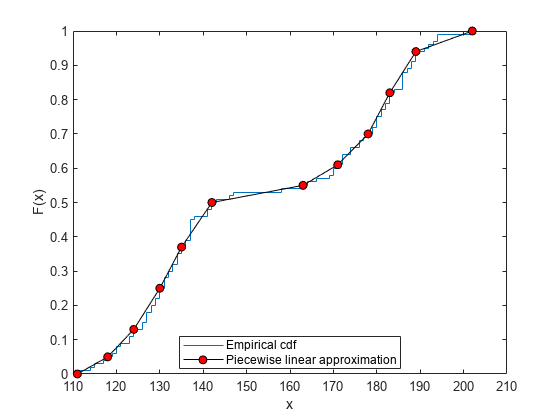
ecdf(___) produces a stairstep graph of
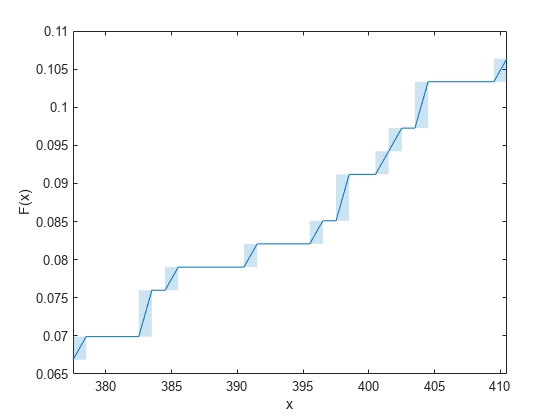
the evaluated function. The function visualizes interval estimates for interval-censored
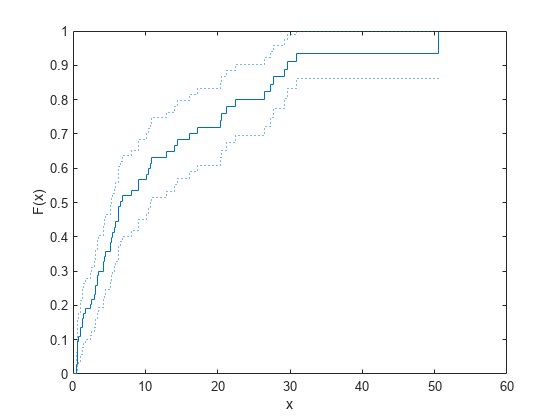
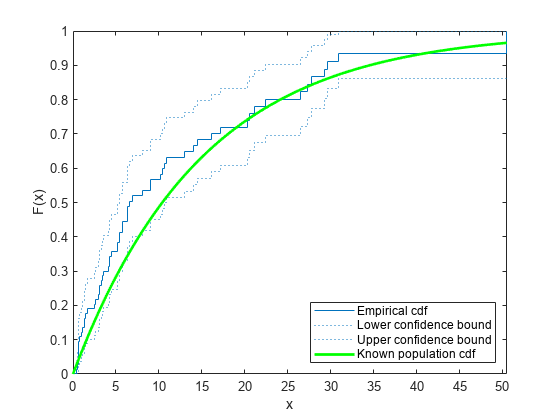
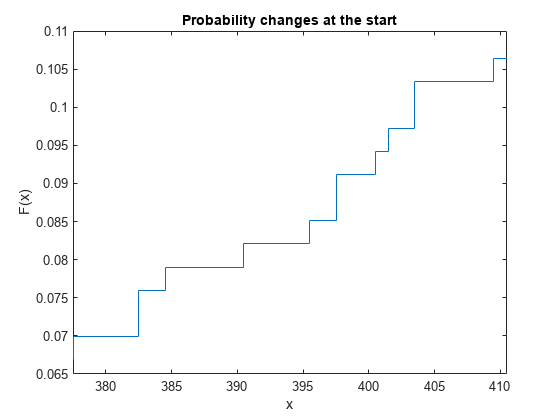
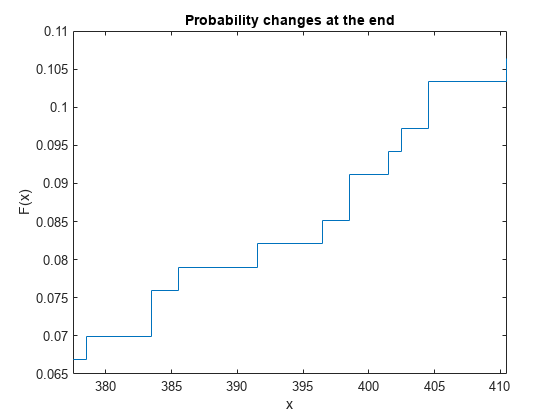
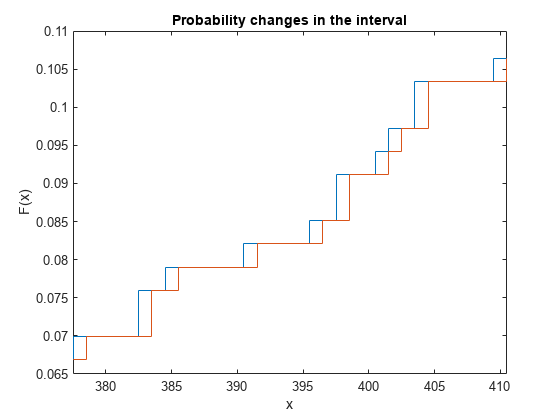
data using shaded rectangles. You can specify
'Bounds','on'
Examples
Input Arguments
Output Arguments
More About
Algorithms
ecdf computes the function values (f) and the
confidence bounds (flo and fup) using different
algorithms, depending on the censorship information. The function type of
f can be the cdf (default), Survivor Function, or Cumulative Hazard Function, as specified by the
Function name-value argument.
| Censorship Type | Algorithm for f | Algorithm for flo and fup |
|---|---|---|
| Right-censored data, which contains fully observed or right-censored observations |
| Use Greenwood’s formula, which is an approximation for the variance of the Kaplan-Meier estimator. The variance estimate is given by |
| Left-censored data, which contains fully observed or left-censored observations | Use the Kaplan-Meier estimator. | Use Greenwood's formula. |
| Double-censored data, which includes both right-censored and left-censored observations | Use Turnbull's algorithm [3][4]. You can specify
the maximum number of iterations ( | Use the Fisher information matrix. |
| Interval-censored data, which includes interval-censored observations |
| Not supported |
References
[1] Cox, D. R., and D. Oakes. Analysis of Survival Data. London: Chapman & Hall, 1984.
[2] Lawless, J. F. Statistical Models and Methods for Lifetime Data. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 2003.
[3] Klein, John P., and Melvin L. Moeschberger. Survival Analysis: Techniques for Censored and Truncated Data. 2nd ed. Statistics for Biology and Health. New York: Springer, 2003.
[4] Turnbull, Bruce W. "Nonparametric Estimation of a Survivorship Function with Doubly Censored Data." Journal of the American Statistical Association 69, No. 345 (1974): 169–73.
[5] Anderson-Bergman, Clifford. "An Efficient Implementation of the EMICM Algorithm for the Interval Censored NPMLE." Journal of Computational and Graphical Statistics 26, no. 2 (April 3, 2017): 463–67.
[6] Ware, James H., and David L. Demets. "Reanalysis of Some Baboon Descent Data." Biometrics 32, no. 2 (June 1976): 459–63.
Extended Capabilities
Version History
Introduced before R2006a