compare
Compare linear mixed-effects models
Syntax
Description
results = compare(lme,altlme)lme and altlme. Both models must use
the same response vector in the fit and lme must be nested in
altlme for a valid theoretical likelihood ratio test.
Always input the smaller model first, and the larger model second.
compare tests the following null and alternate
hypotheses:
H0: Observed response vector is
generated by lme.
H1: Observed response vector is
generated by model altlme.
It is recommended that you fit lme and
altlme using the maximum likelihood (ML) method prior to
model comparison. If you use the restricted maximum likelihood (REML) method,
then both models must have the same fixed-effects design matrix.
To test for fixed effects, use compare with the simulated likelihood ratio
test when lme and altlme are
fit using ML or use the fixedEffects,
anova, or coefTest methods.
results = compare(___,Name,Value)lme and altlme with
additional options specified by one or more Name,Value pair
arguments.
For example, you can check if the first input model is nested in the second input model.
[
returns the results of a simulated likelihood ratio test that compares linear
mixed-effects models results,siminfo]
= compare(lme,altlme,'NSim',nsim)lme and
altlme.
You can fit lme and altlme using ML or
REML. Also, lme does not have to be nested in
altlme. If you use the restricted maximum likelihood
(REML) method to fit the models, then both models must have the same
fixed-effects design matrix.
[
also returns the results of a simulated likelihood ratio test that compares
linear mixed-effects models results,siminfo]
= compare(___,Name,Value)lme and altlme
with additional options specified by one or more Name,Value
pair arguments.
For example, you can change the options for performing the simulated likelihood ratio test, or change the confidence level of the confidence interval for the p-value.
Examples
Test for Random Effects
Load the sample data.
load fluThe flu dataset array has a Date variable, and 10 variables containing estimated influenza rates (in 9 different regions, estimated from Google® searches, plus a nationwide estimate from the CDC).
To fit a linear-mixed effects model, your data must be in a properly formatted dataset array. To fit a linear mixed-effects model with the influenza rates as the responses and region as the predictor variable, combine the nine columns corresponding to the regions into an array. The new dataset array, flu2, must have the response variable, FluRate, the nominal variable, Region, that shows which region each estimate is from, and the grouping variable Date.
flu2 = stack(flu,2:10,'NewDataVarName','FluRate',... 'IndVarName','Region'); flu2.Date = nominal(flu2.Date);
Fit a linear mixed-effects model, with a varying intercept and varying slope for each region, grouped by Date.
altlme = fitlme(flu2,'FluRate ~ 1 + Region + (1 + Region|Date)');Fit a linear mixed-effects model with fixed effects for the region and a random intercept that varies by Date.
lme = fitlme(flu2,'FluRate ~ 1 + Region + (1|Date)');Compare the two models. Also check if lme2 is nested in lme.
compare(lme,altlme,'CheckNesting',true)ans =
THEORETICAL LIKELIHOOD RATIO TEST
Model DF AIC BIC LogLik LRStat deltaDF pValue
lme 11 318.71 364.35 -148.36
altlme 55 -305.51 -77.346 207.76 712.22 44 0
The small -value of 0 indicates that model altlme is significantly better than the simpler model lme.
Test for Fixed and Random Effects
Load the sample data.
load('fertilizer.mat');The dataset array includes data from a split-plot experiment, where soil is divided into three blocks based on the soil type: sandy, silty, and loamy. Each block is divided into five plots, where five different types of tomato plants (cherry, heirloom, grape, vine, and plum) are randomly assigned to these plots. The tomato plants in the plots are then divided into subplots, where each subplot is treated by one of four fertilizers. This is simulated data.
Store the data in a dataset array called ds, for practical purposes, and define Tomato, Soil, and Fertilizer as categorical variables.
ds = fertilizer; ds.Tomato = nominal(ds.Tomato); ds.Soil = nominal(ds.Soil); ds.Fertilizer = nominal(ds.Fertilizer);
Fit a linear mixed-effects model, where Fertilizer and Tomato are the fixed-effects variables, and the mean yield varies by the block (soil type) and the plots within blocks (tomato types within soil types) independently.
lmeBig = fitlme(ds,'Yield ~ Fertilizer * Tomato + (1|Soil) + (1|Soil:Tomato)');Refit the model after removing the interaction term Tomato:Fertilizer and the random-effects term (1 | Soil).
lmeSmall = fitlme(ds,'Yield ~ Fertilizer + Tomato + (1|Soil:Tomato)');Compare the two models using the simulated likelihood ratio test with 1000 replications. You must use this test to test for both fixed- and random-effect terms. Note that both models are fit using the default fitting method, ML. That’s why, there is no restriction on the fixed-effects design matrices. If you use restricted maximum likelihood (REML) method, both models must have identical fixed-effects design matrices.
[table,siminfo] = compare(lmeSmall,lmeBig,'nsim',1000)table =
SIMULATED LIKELIHOOD RATIO TEST: NSIM = 1000, ALPHA = 0.05
Model DF AIC BIC LogLik LRStat pValue Lower Upper
lmeSmall 10 511.06 532 -245.53
lmeBig 23 522.57 570.74 -238.29 14.491 0.57343 0.54211 0.60431
siminfo = struct with fields:
nsim: 1000
alpha: 0.0500
pvalueSim: 0.5734
pvalueSimCI: [0.5421 0.6043]
deltaDF: 13
TH0: [1000x1 double]
The high -value suggests that the larger model, lme is not significantly better than the smaller model, lme2. The smaller values of Akaike and Bayesian Information Criteria for lme2 also support this.
Models with Correlated and Uncorrelated Random Effects
Load the sample data.
load carbig
Fit a linear mixed-effects model for miles per gallon (MPG), with fixed effects for acceleration, horsepower, and the cylinders, and potentially correlated random effects for intercept and acceleration grouped by model year.
First, prepare the design matrices.
X = [ones(406,1) Acceleration Horsepower]; Z = [ones(406,1) Acceleration]; Model_Year = nominal(Model_Year); G = Model_Year;
Now, fit the model using fitlmematrix with the defined design matrices and grouping variables.
lme = fitlmematrix(X,MPG,Z,G,'FixedEffectPredictors',.... {'Intercept','Acceleration','Horsepower'},'RandomEffectPredictors',... {{'Intercept','Acceleration'}},'RandomEffectGroups',{'Model_Year'});
Refit the model with uncorrelated random effects for intercept and acceleration. First prepare the random effects design and the random effects grouping variables.
Z = {ones(406,1),Acceleration};
G = {Model_Year,Model_Year};
lme2 = fitlmematrix(X,MPG,Z,G,'FixedEffectPredictors',....
{'Intercept','Acceleration','Horsepower'},'RandomEffectPredictors',...
{{'Intercept'},{'Acceleration'}},'RandomEffectGroups',...
{'Model_Year','Model_Year'});
Compare lme and lme2 using the simulated likelihood ratio test.
compare(lme2,lme,'CheckNesting',true,'NSim',1000)
ans =
SIMULATED LIKELIHOOD RATIO TEST: NSIM = 1000, ALPHA = 0.05
Model DF AIC BIC LogLik LRStat pValue Lower
lme2 6 2194.5 2218.3 -1091.3
lme 7 2193.5 2221.3 -1089.7 3.0323 0.094905 0.077462
Upper
0.11477
The high 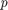 -value indicates that
-value indicates that lme2 is not a significantly better fit than lme.
Simulated Likelihood Ratio Test Using Parallel Computing
Load the sample data.
load('fertilizer.mat')The dataset array includes data from a split-plot experiment, where soil is divided into three blocks based on the soil type: sandy, silty, and loamy. Each block is divided into five plots, where five different types of tomato plants (cherry, heirloom, grape, vine, and plum) are randomly assigned to these plots. The tomato plants in the plots are then divided into subplots, where each subplot is treated by one of four fertilizers. This is simulated data.
Store the data in a table called tbl, and define Tomato, Soil, and Fertilizer as categorical variables.
tbl = dataset2table(fertilizer); tbl.Tomato = categorical(tbl.Tomato); tbl.Soil = categorical(tbl.Soil); tbl.Fertilizer = categorical(tbl.Fertilizer);
Fit a linear mixed-effects model, where Fertilizer and Tomato are the fixed-effects variables, and the mean yield varies by the block (soil type), and the plots within blocks (tomato types within soil types) independently.
lme = fitlme(tbl,'Yield ~ Fertilizer * Tomato + (1|Soil) + (1|Soil:Tomato)');Refit the model after removing the interaction term Tomato:Fertilizer and the random-effects term (1|Soil).
lme2 = fitlme(tbl,'Yield ~ Fertilizer + Tomato + (1|Soil:Tomato)');Create the options structure for LinearMixedModel.
opt = statset('LinearMixedModel')opt = struct with fields:
Display: 'off'
MaxFunEvals: []
MaxIter: 10000
TolBnd: []
TolFun: 1.0000e-06
TolTypeFun: []
TolX: 1.0000e-12
TolTypeX: []
GradObj: []
Jacobian: []
DerivStep: []
FunValCheck: []
Robust: []
RobustWgtFun: []
WgtFun: []
Tune: []
UseParallel: []
UseSubstreams: []
Streams: {}
OutputFcn: []
Change the options for parallel testing.
opt.UseParallel = true;
Start a parallel environment.
mypool = parpool();
Starting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 6).
Compare lme2 and lme using the simulated likelihood ratio test with 1000 replications and parallel computing.
compare(lme2,lme,'nsim',1000,'Options',opt)
ans =
Simulated Likelihood Ratio Test: Nsim = 1000, Alpha = 0.05
Model DF AIC BIC LogLik LRStat pValue Lower Upper
lme2 10 511.06 532 -245.53
lme 23 522.57 570.74 -238.29 14.491 0.53447 0.503 0.56573
The high -value suggests that the larger model, lme is not significantly better than the smaller model, lme2. The smaller values of AIC and BIC for lme2 also support this.
Input Arguments
lme — Linear mixed-effects model
LinearMixedModel object
Linear mixed-effects model, specified as a LinearMixedModel object constructed using fitlme or fitlmematrix.
altlme — Alternative linear mixed-effects model
LinearMixedModel object
Alternative linear mixed-effects model fit to the same response vector but
with different model specifications, specified as a
LinearMixedModel object. lme
must be nested in altlme, that is, lme
should be obtained from altlme by setting some parameters
to fixed values, such as 0. You can create a linear mixed-effects object
using fitlme or fitlmematrix.
nsim — Number of replications for simulations
positive integer number
Number of replications for simulations in the simulated likelihood ratio
test, specified as a positive integer number. You must specify
nsim to do a simulated likelihood ratio test.
Example: 'NSim',1000
Data Types: double | single
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: results =
compare(lme,altlme,'CheckNesting',true)
Alpha — Significance level
0.05 (default) | scalar value in the range 0 to 1
Significance level, specified as the comma-separated pair consisting of
'Alpha' and a scalar value in the range 0 to 1. For a value α,
the confidence level is 100*(1–α)%.
For example, for 99% confidence intervals, you can specify the confidence level as follows.
Example: 'Alpha',0.01
Data Types: single | double
Options — Options for performing simulated likelihood ratio test
structure
Options for performing the simulated likelihood ratio test in
parallel, specified as the comma-separated pair consisting of
'Options', and a structure created by
statset('LinearMixedModel').
These options require Parallel Computing Toolbox™.
compare uses the following fields.
'UseParallel' |
You need Parallel Computing Toolbox for parallel computation. |
'UseSubstreams' |
|
'Streams' |
|
For information on parallel statistical computing at the command line, enter
help parallelstatsData Types: struct
CheckNesting — Indicator to check nesting between two models
false (default) | true
Indicator to check
nesting between two models, specified as the comma-separated
pair consisting of 'CheckNesting' and one of the
following.
false | Default. No checks. |
true | compare checks if the smaller
model lme is nested in the bigger
model altlme. |
lme must be nested in the alternate model
altlme for a valid theoretical likelihood ratio
test. compare returns an error message if
the nesting requirements are not satisfied.
Although valid for both tests, the nesting requirements are weaker for the simulated likelihood ratio test.
Example: 'CheckNesting',true
Data Types: single | double
Output Arguments
results — Results of likelihood ratio test or simulated likelihood ratio test
dataset array
Results of the likelihood ratio test or simulated likelihood ratio test,
returned as a dataset array with two rows. The first row is for
lme, and the second row is for
altlme. The columns of results
depend on whether the test is a likelihood ratio or a simulated likelihood
ratio test.
If you use the likelihood ratio test, then
resultscontains the following columns.ModelName of the model DFDegrees of freedom, that is, the number of free parameters in the model AICAkaike information criterion for the model BICBayesian information criterion for the model LogLikMaximized log likelihood for the model LRStatLikelihood ratio test statistic for comparing altlmeversuslmedeltaDFDFforaltlmeminusDFforlmepValuep-value for the likelihood ratio test If you use the simulated likelihood ratio test, then
resultscontains the following columns.ModelName of the model DFDegrees of freedom, that is, the number of free parameters in the model LogLikMaximized log likelihood for the model LRStatLikelihood ratio test statistic for comparing altlmeversuslmepValuep-value for the likelihood ratio test LowerLower limit of the confidence interval for pValueUpperUpper limit of the confidence interval for pValue
siminfo — Simulation output
structure
Simulation output, returned as a structure with the following fields.
nsim | Value set for nsim. |
alpha | Value set for 'Alpha'. |
pValueSim | Simulation-based p-value. |
pValueSimCI | Confidence interval for pValueSim. The
first element of the vector is the lower limit and the
second element of the vector contains the upper
limit. |
deltaDF | The number of free parameters in
altlme minus the number of free
parameters in lme. DF
for altlme minus DF
for lme. |
THO | A vector of simulated likelihood ratio test statistics
under the null hypothesis that the model
lme generated the observed response
vector y. |
More About
Likelihood Ratio Test
Under the null hypothesis
H0, the observed likelihood ratio test
statistic has an approximate chi-squared reference distribution with degrees of
freedom deltaDF. When comparing two models,
compare computes the p-value for the
likelihood ratio test by comparing the observed likelihood ratio test statistic with
this chi-squared reference distribution.
The p-values obtained using the likelihood ratio test can be
conservative when testing for the presence or absence of random-effects terms and
anticonservative when testing for the presence or absence of fixed-effects terms.
Hence, use the fixedEffects, anova, or
coefTest method or the simulated likelihood ratio test while
testing for fixed effects.
Simulated Likelihood Ratio Test
To perform the simulated likelihood ratio test,
compare first generates the reference distribution of the
likelihood ratio test statistic under the null hypothesis. Then, it assesses the
statistical significance of the alternate model by comparing the observed likelihood
ratio test statistic to this reference distribution.
compare produces the simulated reference distribution of the
likelihood ratio test statistic under the null hypothesis as follows:
Generate random data
ysimfrom the fitted modellme.Fit the model specified in
lmeand alternate modelaltlmeto the simulated dataysim.Calculate the likelihood ratio test statistic using results from step 2 and store the value.
Repeat step 1 to 3
nsimtimes.
Then, compare computes the p-value for the
simulated likelihood ratio test by comparing the observed likelihood ratio test
statistic with the simulated reference distribution. The p-value
estimate is the ratio of the number of times the simulated likelihood ratio test
statistic is equal to or exceeds the observed value plus one, to the number of
replications plus one.
Suppose the observed likelihood ratio statistic is T, and the simulated reference distribution is stored in vector TH0. Then,
To account for the uncertainty in the simulated reference distribution,
compare computes a 100*(1 – α)% confidence interval for the
true p-value.
You can use the simulated likelihood ratio test to compare arbitrary linear
mixed-effects models. That is, when you are using the simulated likelihood ratio
test, lme does not have to be nested within
altlme, and you can fit lme and
altlme using either maximum likelihood (ML) or restricted
maximum likelihood (REML) methods. If you use the restricted maximum likelihood
(REML) method to fit the models, then both models must have the same fixed-effects
design matrix.
Nesting Requirements
The 'CheckNesting','True' name-value pair argument checks the
following requirements.
For a simulated likelihood ratio test:
You must use the same method to fit both models (
lmeandaltlme).comparecannot compare a model fit using ML to a model fit using REML.You must fit both models to the same response vector.
If you use REML to fit
lmeandaltlme, then both models must have the same fixed-effects design matrix.The maximized log likelihood or restricted log likelihood of the bigger model (
altlme) must be greater than or equal to that of the smaller model (lme).
For a theoretical test, 'CheckNesting','True' checks all the
requirements listed for a simulated likelihood ratio test and the following:
Weight vectors you use to fit
lmeandaltlmemust be identical.If you use ML to fit
lmeandaltlme, the fixed-effects design matrix of the bigger model (altlme) must contain that of the smaller model (lme).The random-effects design matrix of the bigger model (
altlme) must contain that of the smaller model (lme).
Akaike and Bayesian Information Criteria
Akaike information criterion (AIC) is AIC = –2*logLM + 2*(nc + p + 1), where logLM is the maximized log likelihood (or maximized restricted log likelihood) of the model, and nc + p + 1 is the number of parameters estimated in the model. p is the number of fixed-effects coefficients, and nc is the total number of parameters in the random-effects covariance excluding the residual variance.
Bayesian information criterion (BIC) is BIC = –2*logLM + ln(neff)*(nc + p + 1), where logLM is the maximized log likelihood (or maximized restricted log likelihood) of the model, neff is the effective number of observations, and (nc + p + 1) is the number of parameters estimated in the model.
If the fitting method is maximum likelihood (ML), then neff = n, where n is the number of observations.
If the fitting method is restricted maximum likelihood (REML), then neff = n – p.
A lower value of deviance indicates a better fit. As the value of deviance decreases, both AIC and BIC tend to decrease. Both AIC and BIC also include penalty terms based on the number of parameters estimated, p. So, when the number of parameters increase, the values of AIC and BIC tend to increase as well. When comparing different models, the model with the lowest AIC or BIC value is considered as the best fitting model.
Deviance
LinearMixedModel computes the deviance of
model M as minus two times the loglikelihood of
that model. Let LM denote
the maximum value of the likelihood function for model M.
Then, the deviance of model M is
A lower value of deviance indicates a better fit. Suppose M1 and M2 are two different models, where M1 is nested in M2. Then, the fit of the models can be assessed by comparing the deviances Dev1 and Dev2 of these models. The difference of the deviances is
Usually, the asymptotic distribution of this difference has a chi-square distribution with
degrees of freedom v equal to the number of parameters that are estimated
in one model but fixed (typically at 0) in the other. That is, it is equal to the difference
in the number of parameters estimated in M1 and
M2. You can get the p-value for this test
using 1 – chi2cdf(Dev,V), where Dev =
Dev2 –
Dev1.
However, in mixed-effects models, when some variance components fall on the boundary of the parameter space, the asymptotic distribution of this difference is more complicated. For example, consider the hypotheses
H0: D is a q-by-q symmetric positive semidefinite matrix.
H1: D is a (q+1)-by-(q+1) symmetric positive semidefinite matrix.
That is, H1 states that the last row and column of D are different from zero. Here, the bigger model M2 has q + 1 parameters and the smaller model M1 has q parameters. And Dev has a 50:50 mixture of χ2q and χ2(q + 1) distributions (Stram and Lee, 1994).
References
[1] Hox, J. Multilevel Analysis, Techniques and Applications. Lawrence Erlbaum Associates, Inc., 2002.
[2] Stram D. O. and J. W. Lee. “Variance components testing in the longitudinal mixed-effects model”. Biometrics, Vol. 50, 4, 1994, pp. 1171–1177.
Extended Capabilities
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2013b
See Also
LinearMixedModel | fitlme | fitlmematrix | anova | fixedEffects | randomEffects | covarianceParameters
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)