multcompare
Multiple comparison test
Syntax
Description
c = multcompare(stats)c of the pairwise comparison results from a multiple
comparison test using the information contained in the stats structure.
multcompare also displays an interactive graph of the estimates and
comparison intervals. Each group mean is represented by a symbol, and the interval is
represented by a line extending out from the symbol. Two group means are significantly different
if their intervals are disjoint; they are not significantly different if their intervals
overlap. If you use your mouse to select any group, then the graph will highlight all other
groups that are significantly different, if any.
c = multcompare(stats,Name,Value)
Examples
Multiple Comparisons of Group Means
Load the carsmall data set.
load carsmallThe data contains miles per gallon (MPG) measurements for different makes and models of cars, grouped by the country of origin (Origin) and other vehicle characteristics.
Perform a one-way analysis of variance (ANOVA) to see if the MPG values of the cars are different depending on the country of origin.
[p,t,stats] = anova1(MPG,Origin);
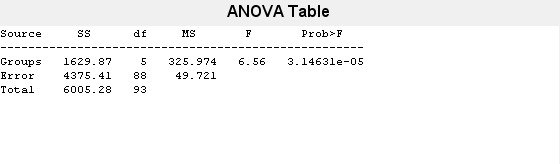
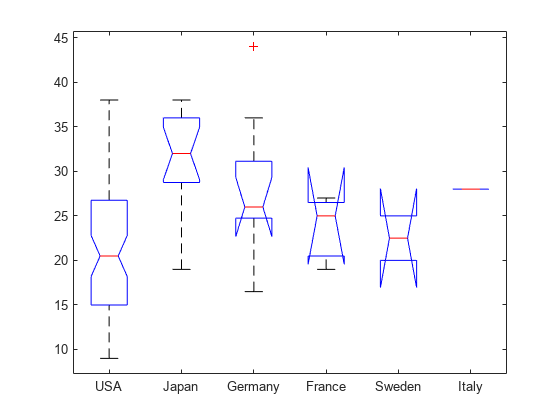
The small p-value (value in the column Prob>F) indicates that group mean differences are significant. However, the ANOVA results do not indicate which groups have different means. You can perform pairwise comparisons using a multiple comparison test to identify the groups that have significantly different means.
Perform a multiple comparison test of the group means.
[c,m,h,gnames] = multcompare(stats);
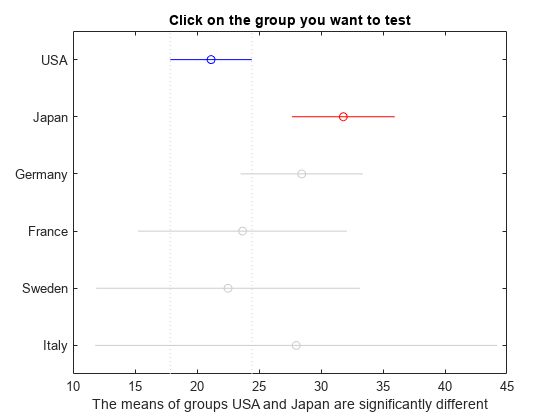
multcompare displays the estimates with comparison intervals around them. You can click the graph of any country to compare its mean to those of other countries.
Display the mean estimates, standard errors, and corresponding group names in a table.
tbl = array2table(m,"RowNames",gnames, ... "VariableNames",["Mean","Standard Error"])
tbl=6×2 table
Mean Standard Error
______ ______________
USA 21.133 0.88141
Japan 31.8 1.8206
Germany 28.444 2.3504
France 23.667 4.0711
Sweden 22.5 4.986
Italy 28 7.0513
Multiple Comparisons Against Control Group
Perform a multiple comparison test against a control group using Dunnett's test, and compare the results to the pairwise comparison results from Tukey’s honestly significant difference procedure.
Load the carsmall data set.
load carsmallThe data contains miles per gallon (MPG) measurements for different makes and models of cars, grouped by the country of origin (Origin) and other vehicle characteristics.
Perform a one-way ANOVA to compare the mileage of the cars across the groups defined by their countries of origin.
[~,~,stats] = anova1(MPG,Origin,"off");Display the names of the groups.
stats.gnames
ans = 6x1 cell
{'USA' }
{'Japan' }
{'Germany'}
{'France' }
{'Sweden' }
{'Italy' }
According to the multiple comparison results for all distinct pairs of groups in the Multiple Comparisons of Group Means example, USA and Japan have significantly different means. The example uses the default test, Tukey’s honestly significant difference procedure.
Compare the group means against a control group by using Dunnett's test.
Specify CriticalValueType as "dunnett" to perform Dunnett's test. multcompare selects the first group (USA) as the control group by default. You can select a different control group by using the ControlGroup name-value argument.
[results,~,~,gnames] = multcompare(stats,"CriticalValueType","dunnett");
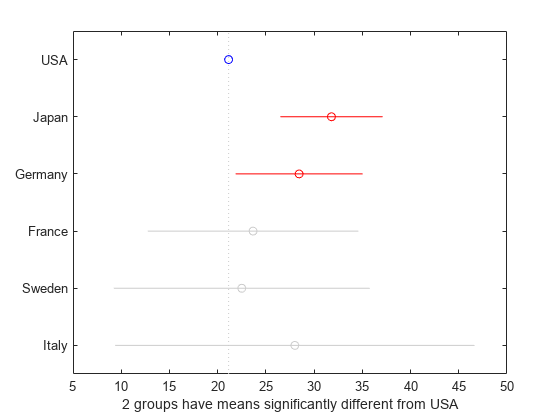
In the figure, the blue circle indicates the mean of the control group. The red circles and bars represent the means and confidence intervals for the groups with significantly different means from the mean of the control group. Note that the red bars do not cross the dotted vertical line representing the mean of the control group. Groups that do not have significantly different means appear in grey.
Dunnett's test identifies that two groups, Japan and Germany, have means that are significantly different from the mean of the USA (control group). Note that the default procedure (Tukey’s honestly significant difference procedure) did not identify Germany in the Multiple Comparisons of Group Means example. The difference in the results is related to the different levels of conservativeness in the two comparison tests. Dunnett's test is less conservative than the default procedure because the test considers only the comparisons against a control group. The default procedure performs pairwise comparisons for all distinct pairs of groups.
Display the multiple comparison results and the corresponding group names in a table.
tbl = array2table(results,"VariableNames", ... ["Group","Control Group","Lower Limit","Difference","Upper Limit","P-value"]); tbl.("Group") = gnames(tbl.("Group")); tbl.("Control Group") = gnames(tbl.("Control Group"))
tbl=5×6 table
Group Control Group Lower Limit Difference Upper Limit P-value
___________ _____________ ___________ __________ ___________ _________
{'Japan' } {'USA'} 5.3649 10.667 15.969 4.727e-06
{'Germany'} {'USA'} 0.73151 7.3116 13.892 0.022346
{'France' } {'USA'} -8.3848 2.5339 13.453 0.97912
{'Sweden' } {'USA'} -11.905 1.3672 14.64 0.99953
{'Italy' } {'USA'} -11.76 6.8672 25.495 0.86579
Multiple Comparisons for Two-Way ANOVA
Load the sample data.
load popcorn
popcornpopcorn = 6×3
5.5000 4.5000 3.5000
5.5000 4.5000 4.0000
6.0000 4.0000 3.0000
6.5000 5.0000 4.0000
7.0000 5.5000 5.0000
7.0000 5.0000 4.5000
The data is from a study of popcorn brands and popper types (Hogg 1987). The columns of the matrix popcorn are brands (Gourmet, National, and Generic). The rows are popper types oil and air. The first three rows correspond to the oil popper, and the last three rows correspond to the air popper. In the study, researchers popped a batch of each brand three times with each popper. The values are the yield in cups of popped popcorn.
Perform a two-way ANOVA. Also compute the statistics that you need to perform a multiple comparison test on the main effects.
[~,~,stats] = anova2(popcorn,3,"off")stats = struct with fields:
source: 'anova2'
sigmasq: 0.1389
colmeans: [6.2500 4.7500 4]
coln: 6
rowmeans: [4.5000 5.5000]
rown: 9
inter: 1
pval: 0.7462
df: 12
The stats structure includes
The mean squared error (
sigmasq)The estimates of the mean yield for each popcorn brand (
colmeans)The number of observations for each popcorn brand (
coln)The estimate of the mean yield for each popper type (
rowmeans)The number of observations for each popper type (
rown)The number of interactions (
inter)The p-value that shows the significance level of the interaction term (
pval)The error degrees of freedom (
df).
Perform a multiple comparison test to see if the popcorn yield differs between pairs of popcorn brands (columns).
c1 = multcompare(stats);
Note: Your model includes an interaction term. A test of main effects can be difficult to interpret when the model includes interactions.
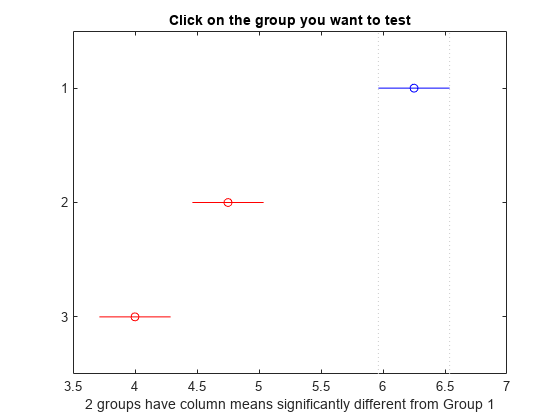
The figure shows the multiple comparisons of the means. By default, the group 1 mean is highlighted and the comparison interval is in blue. Because the comparison intervals for the other two groups do not intersect with the intervals for the group 1 mean, they are highlighted in red. This lack of intersection indicates that both means are different than group 1 mean. Select other group means to confirm that all group means are significantly different from each other.
Display the multiple comparison results in a table.
tbl1 = array2table(c1,"VariableNames", ... ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])
tbl1=3×6 table
Group A Group B Lower Limit A-B Upper Limit P-value
_______ _______ ___________ ____ ___________ __________
1 2 0.92597 1.5 2.074 4.1188e-05
1 3 1.676 2.25 2.824 6.1588e-07
2 3 0.17597 0.75 1.324 0.011591
The first two columns of c1 show the groups that are compared. The fourth column shows the difference between the estimated group means. The third and fifth columns show the lower and upper limits for 95% confidence intervals for the true mean difference. The sixth column contains the p-value for a hypothesis test that the corresponding mean difference is equal to zero. All p-values are very small, which indicates that the popcorn yield differs across all three brands.
Perform a multiple comparison test to see the popcorn yield differs between the two popper types (rows).
c2 = multcompare(stats,"Estimate","row");
Note: Your model includes an interaction term. A test of main effects can be difficult to interpret when the model includes interactions.
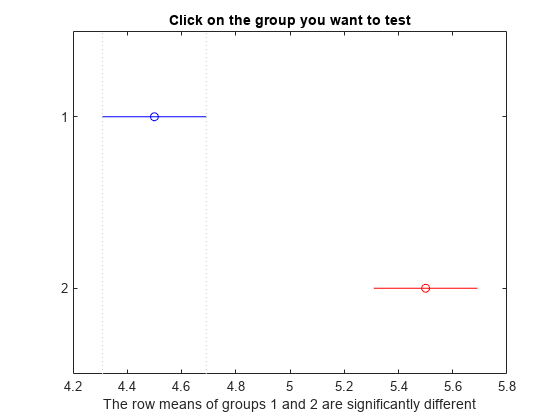
tbl2 = array2table(c2,"VariableNames", ... ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])
tbl2=1×6 table
Group A Group B Lower Limit A-B Upper Limit P-value
_______ _______ ___________ ___ ___________ __________
1 2 -1.3828 -1 -0.61722 0.00010037
The small p-value indicates that the popcorn yield differs between the two popper types (air and oil). The figure shows the same results. The disjoint comparison intervals indicate that the group means are significantly different from each other.
Multiple Comparisons for Three-Way ANOVA
Load the sample data.
y = [52.7 57.5 45.9 44.5 53.0 57.0 45.9 44.0]'; g1 = [1 2 1 2 1 2 1 2]; g2 = ["hi" "hi" "lo" "lo" "hi" "hi" "lo" "lo"]; g3 = ["may" "may" "may" "may" "june" "june" "june" "june"];
y is the response vector and g1, g2, and g3 are the grouping variables (factors). Each factor has two levels, and every observation in y is identified by a combination of factor levels. For example, observation y(1) is associated with level 1 of factor g1, level hi of factor g2, and level may of factor g3. Similarly, observation y(6) is associated with level 2 of factor g1, level hi of factor g2, and level june of factor g3.
Test if the response is the same for all factor levels. Also compute the statistics required for multiple comparison tests.
[~,~,stats] = anovan(y,{g1 g2 g3},"Model","interaction", ...
"Varnames",["g1","g2","g3"]);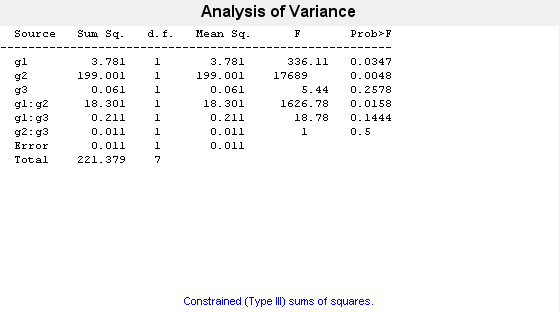
The p-value of 0.2578 indicates that the mean responses for levels may and june of factor g3 are not significantly different. The p-value of 0.0347 indicates that the mean responses for levels 1 and 2 of factor g1 are significantly different. Similarly, the p-value of 0.0048 indicates that the mean responses for levels hi and lo of factor g2 are significantly different.
Perform a multiple comparison test to find out which groups of factors g1 and g2 are significantly different.
[results,~,~,gnames] = multcompare(stats,"Dimension",[1 2]);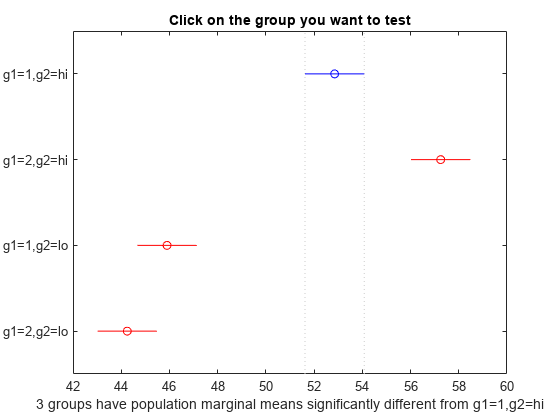
You can test the other groups by clicking on the corresponding comparison interval for the group. The bar you click on turns to blue. The bars for the groups that are significantly different are red. The bars for the groups that are not significantly different are gray. For example, if you click on the comparison interval for the combination of level 1 of g1 and level lo of g2, the comparison interval for the combination of level 2 of g1 and level lo of g2 overlaps, and is therefore gray. Conversely, the other comparison intervals are red, indicating significant difference.
Display the multiple comparison results and the corresponding group names in a table.
tbl = array2table(results,"VariableNames", ... ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"]); tbl.("Group A")=gnames(tbl.("Group A")); tbl.("Group B")=gnames(tbl.("Group B"))
tbl=6×6 table
Group A Group B Lower Limit A-B Upper Limit P-value
______________ ______________ ___________ _____ ___________ _________
{'g1=1,g2=hi'} {'g1=2,g2=hi'} -6.8604 -4.4 -1.9396 0.027249
{'g1=1,g2=hi'} {'g1=1,g2=lo'} 4.4896 6.95 9.4104 0.016983
{'g1=1,g2=hi'} {'g1=2,g2=lo'} 6.1396 8.6 11.06 0.013586
{'g1=2,g2=hi'} {'g1=1,g2=lo'} 8.8896 11.35 13.81 0.010114
{'g1=2,g2=hi'} {'g1=2,g2=lo'} 10.54 13 15.46 0.0087375
{'g1=1,g2=lo'} {'g1=2,g2=lo'} -0.8104 1.65 4.1104 0.07375
The multcompare function compares the combinations of groups (levels) of the two grouping variables, g1 and g2. For example, the first row of the matrix shows that the combination of level 1 of g1 and level hi of g2 has the same mean response values as the combination of level 2 of g1 and level hi of g2. The p-value corresponding to this test is 0.0272, which indicates that the mean responses are significantly different. You can also see this result in the figure. The blue bar shows the comparison interval for the mean response for the combination of level 1 of g1 and level hi of g2. The red bars are the comparison intervals for the mean response for other group combinations. None of the red bars overlap with the blue bar, which means the mean response for the combination of level 1 of g1 and level hi of g2 is significantly different from the mean response for other group combinations.
Input Arguments
stats — Test data
structure
Test data, specified as a structure. You can create a structure using one of the following functions:
multcompare does not support multiple comparisons
using anovan output for a model that includes
random or nested effects. The calculations for a random effects model
produce a warning that all effects are treated as fixed. Nested models
are not accepted.
Data Types: struct
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Alpha=0.01,CriticalValueType="bonferroni",Display="off" computes
the Bonferroni critical values, conducts the hypothesis tests at the 1% significance level, and
omits the interactive display.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: "Alpha",0.01,"CriticalValueType","bonferroni","Display","off"
Alpha — Significance level
0.05 (default) | scalar value in the range (0,1)
Significance level of the multiple comparison test, specified as a scalar value in the range
(0,1). The value specified for Alpha determines the 100 × (1 – α) confidence levels of the intervals returned in the matrix
c and in the figure.
Example: "Alpha",0.01
Data Types: single | double
Approximate — Flag to compute critical value for Dunnett's test using approximate method
true or 1 | false or 0
Flag to compute a critical value for Dunnett's test using an approximate method,
specified as logical 1 (true) or
0 (false).
The multcompare function finds a critical value for Dunnett's
test by integrating the multivariate t distribution. The
computation can be slow for multiway (n-way) ANOVA if
n is large. To speed up the computation, you can use an
approximate method ([5]) by specifying
Approximate as true. The approximate method
involves randomness. If you want to reproduce the results, set the random seed by
using the rng function before calling
multcompare.
The default value is true if the source of
stats is anovan. Otherwise, the default value is false.
This argument is valid only when CriticalValueType is
"dunnett".
Example: "Approximate",true
Data Types: logical
ControlGroup — Index of control group for Dunnett's test
1 (default) | positive integer value
Index of the control group for Dunnett's test, specified as a positive integer value.
Specify one of the groups compared by the multcompare function as
the control group. Assume that you specify ControlGroup as
idx. This table shows the control group value, which depends on
the source of stats.
Source of stats | Control Group |
|---|---|
anova1 |
|
anova2 |
|
anovan | If you specify |
aoctool |
|
friedman |
|
kruskalwallis |
|
This argument is valid only when CriticalValueType is
"dunnett".
Example: "ControlGroup",3
Data Types: single | double
CriticalValueType — Type of critical value
"tukey-kramer" (default) | "lsd" | "dunnett" | "dunn-sidak" | "bonferroni" | "scheffe"
Type of the critical value to use for the multiple comparison test, specified as one of the following.
| Value | Description |
|---|---|
"lsd" | Fisher's least significant difference procedure |
"dunnett" | Dunnett's test |
"tukey-kramer" or "hsd" (default) | Tukey’s honestly significant difference procedure |
"dunn-sidak" | Dunn & Sidák’s approach |
"bonferroni" | Bonferroni method |
"scheffe" | Scheffe’s procedure |
The table lists the critical value types in order of conservativeness, from least to most conservative. Each test provides a different level of protection against the multiple comparison problem.
"lsd"does not provide any protection."dunnett"provides protection for comparisons against a control group."tukey-kramer","dunn-sidak", and"bonferroni"provide protection for pairwise comparisons."scheffe"provides protection for pairwise comparisons and comparisons of all linear combinations of the estimates.
For more information, see Multiple Comparison Procedures.
Example: "CriticalValueType","bonferroni"
Data Types: string | char
Display — Display toggle
"on" (default) | "off"
Display toggle, specified as either "on" or "off". If
you specify "on", then multcompare displays a graph
of the estimates and their comparison intervals. If you specify "off",
then multcompare omits the graph.
Example: "Display","off"
Data Types: string | char
Dimension — Dimension over which to calculate marginal means
1 (default) | positive integer value | vector of positive integer values
Dimension or dimensions over which to calculate the population marginal means, specified as a
positive integer value, or a vector of such values. If you specify
CriticalValueType as "dunnett", then you can
specify only one dimension.
This argument is valid only when you create the input structure stats
using the function anovan.
For example, if you specify Dimension as 1, then
multcompare compares the means for each value of the first grouping
variable, adjusted by removing effects of the other grouping variables as if the design were
balanced. If you specify Dimension as [1,3], then
multcompare computes the population marginal means for each combination
of the first and third grouping variables, removing effects of the second grouping variable.
If you fit a singular model, some cell means may not be estimable and any population marginal
means that depend on those cell means will have the value NaN.
Population marginal means are described by Milliken and Johnson (1992) and by Searle, Speed,
and Milliken (1980). The idea behind population marginal means is to remove any effect of an
unbalanced design by fixing the values of the factors specified by
Dimension, and averaging out the effects of other factors as if each
factor combination occurred the same number of times. The definition of population marginal
means does not depend on the number of observations at each factor combination. For designed
experiments where the number of observations at each factor combination has no meaning,
population marginal means can be easier to interpret than simple means ignoring other
factors. For surveys and other studies where the number of observations at each combination
does have meaning, population marginal means may be harder to interpret.
Example: "Dimension",[1,3]
Data Types: single | double
Estimate — Estimates to be compared
"column" (default) | "row" | "slope" | "intercept" | "pmm"
Estimates to be compared, specified as an allowable value. The allowable values for
Estimate depend on the function used to generate the input structure
stats, according to the following table.
| Function | Values |
|---|---|
anova1 | None. |
anova2 | Either |
anovan | None. |
aoctool |
|
friedman | None. |
kruskalwallis | None. |
Example: "Estimate","row"
Data Types: string | char
Output Arguments
c — Matrix of multiple comparison results
matrix of scalar values
Matrix of multiple comparison results, returned as an p-by-6 matrix of scalar values, where p is the number of pairs of groups. Each row of the matrix contains the result of one paired comparison test. Columns 1 and 2 contain the indices of the two samples being compared. Column 3 contains the lower confidence interval, column 4 contains the estimate, and column 5 contains the upper confidence interval. Column 6 contains the p-value for the hypothesis test that the corresponding mean difference is not equal to 0.
For example, suppose one row contains the following entries.
2.0000 5.0000 1.9442 8.2206 14.4971 0.0432
These numbers indicate that the mean of group 2 minus the mean of group 5 is estimated to be 8.2206, and a 95% confidence interval for the true difference of the means is [1.9442, 14.4971]. The p-value for the corresponding hypothesis test that the difference of the means of groups 2 and 5 is significantly different from zero is 0.0432.
In this example the confidence interval does not contain 0, so the difference is significant at the 5% significance level. If the confidence interval did contain 0, the difference would not be significant. The p-value of 0.0432 also indicates that the difference of the means of groups 2 and 5 is significantly different from 0.
m — Matrix of estimates
matrix of scalar values
Matrix of the estimates, returned as a matrix of scalar values.
The first column of m contains the estimated values
of the means (or whatever statistics are being compared) for each
group, and the second column contains their standard errors.
h — Handle to the figure
handle
Handle to the figure containing the interactive graph, returned as a handle. The title of this graph contains instructions for interacting with the graph, and the x-axis label contains information about which means are significantly different from the selected mean. If you plan to use this graph for presentation, you may want to omit the title and the x-axis label. You can remove them using interactive features of the graph window, or you can use the following commands.
title("") xlabel("")
gnames — Group names
cell array of character vectors
Group names, returned as a cell array of character vectors.
Each row of gnames contains the name of a group.
More About
Multiple Comparison Tests
Analysis of variance compares the means of several groups to test the hypothesis that they are all equal, against the general alternative that they are not all equal. Sometimes this alternative may be too general. You may need information about which pairs of means are significantly different, and which are not. A multiple comparison test can provide this information.
When you perform a simple t-test of one group mean against another, you
specify a significance level that determines the cutoff value of the
t-statistic. For example, you can specify the value
alpha = 0.05 to ensure that when there is
no real difference, you will incorrectly find a significant difference no more than 5% of
the time. When there are many group means, there are also many pairs to compare. If you
applied an ordinary t-test in this situation, the
alpha value would apply to each comparison, so the chance of
incorrectly finding a significant difference would increase with the number of comparisons.
Multiple comparison procedures are designed to provide an upper bound on the probability
that any comparison will be incorrectly found significant.
Null and Alternative Hypotheses
The multcompare function
examines different sets of null hypotheses (H0) and
alternative hypotheses (H1) depending on the type of
critical value specified by the CriticalValueType name-value argument.
Dunnett's test (
CriticalValueTypeis"dunnett") performs multiple comparisons against a control group. Therefore, the null and alternative hypotheses for a comparison against the control group arewhere mi and m0 are estimates for group i and the control group, respectively. The function examines H0 and H1 multiple times for all noncontrol groups.
For the other tests,
multcompareperforms multiple pairwise comparisons for all distinct pairs of groups. The null and alternative hypotheses of a pairwise comparison between group i and j are
References
[1] Hochberg, Y., and A. C. Tamhane. Multiple Comparison Procedures. Hoboken, NJ: John Wiley & Sons, 1987.
[2] Milliken, G. A., and D. E. Johnson. Analysis of Messy Data, Volume I: Designed Experiments. Boca Raton, FL: Chapman & Hall/CRC Press, 1992.
[3] Searle, S. R., F. M. Speed, and G. A. Milliken. “Population marginal means in the linear model: an alternative to least-squares means.” American Statistician. 1980, pp. 216–221.
[4] Dunnett, Charles W. “A Multiple Comparison Procedure for Comparing Several Treatments with a Control.” Journal of the American Statistical Association, vol. 50, no. 272, Dec. 1955, pp. 1096–121.
[5] Krishnaiah, Paruchuri R., and J. V. Armitage. "Tables for multivariate t distribution." Sankhyā: The Indian Journal of Statistics, Series B (1966): 31-56.
Version History
Introduced before R2006aR2022a: CType has been renamed to CriticalValueType
The CType name-value argument has been renamed to
CriticalValueType to better indicate its functionality.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)