nnmf
Nonnegative matrix factorization
Description
[
factors the n-by-m matrix W,H] = nnmf(A,k)A
into nonnegative factors W
(n-by-k) and H
(k-by-m). The factorization is not exact;
W*H is a lower-rank approximation to A.
The factors W and H minimize the root mean
square residual D between A and
W*H.
D = norm(A - W*H,'fro')/sqrt(n*m)The factorization uses an iterative algorithm starting with random initial values
for W and H. Because the root mean square
residual D might have local minima, repeated factorizations might
yield different W and H. Sometimes the
algorithm converges to a solution of lower rank than k, which can
indicate that the result is not optimal.
[
modifies the factorization using one or more name-value pair arguments. For example,
you can request repeated factorizations by setting W,H] = nnmf(A,k,Name,Value)'Replicates'
to an integer value greater than 1.
Examples
Nonnegative Rank-Two Approximation and Biplot
Load the sample data.
load fisheririsCompute a nonnegative rank-two approximation of the measurements of the four variables in Fisher's iris data.
rng(1) % For reproducibility
[W,H] = nnmf(meas,2);
HH = 2×4
0.6945 0.2856 0.6220 0.2218
0.8020 0.5683 0.1834 0.0149
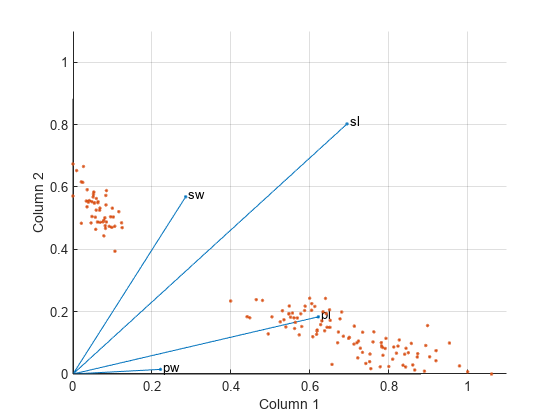
The first and third variables in meas (sepal length and petal length, with coefficients 0.6945 and 0.6220, respectively) provide relatively strong weights to the first column of W . The first and second variables in meas (sepal length and sepal width, with coefficients 0.8020 and 0.5683, respectively) provide relatively strong weights to the second column of W.
Create a biplot of the data and the variables in meas in the column space of W.
biplot(H','Scores',W,'VarLabels',{'sl','sw','pl','pw'}); axis([0 1.1 0 1.1]) xlabel('Column 1') ylabel('Column 2')
Change Algorithm
Starting from a random array X with rank 20, try a few iterations at several replicates using the multiplicative algorithm.
rng default % For reproducibility X = rand(100,20)*rand(20,50); opt = statset('MaxIter',5,'Display','final'); [W0,H0] = nnmf(X,5,'Replicates',10,... 'Options',opt,... 'Algorithm','mult');
rep iteration rms resid |delta x|
1 5 0.560887 0.0245182
2 5 0.66418 0.0364471
3 5 0.609125 0.0358355
4 5 0.608894 0.0415491
5 5 0.619291 0.0455135
6 5 0.621549 0.0299965
7 5 0.640549 0.0438758
8 5 0.673015 0.0366856
9 5 0.606835 0.0318931
10 5 0.633526 0.0319591
Final root mean square residual = 0.560887
Continue with more iterations from the best of these results using alternating least squares.
opt = statset('Maxiter',1000,'Display','final'); [W,H] = nnmf(X,5,'W0',W0,'H0',H0,... 'Options',opt,... 'Algorithm','als');
rep iteration rms resid |delta x|
1 24 0.257336 0.00271859
Final root mean square residual = 0.257336
Input Arguments
A — Matrix to factorize
real matrix
Matrix to factorize, specified as a real matrix.
Example: rand(20,30)
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: [W,H] = nnmf(A,k,'Algorithm','mult','Replicates',10)
chooses the multiplicative update algorithm and ten replicates to improve the
result
Algorithm — Factorization algorithm
'als' (default) | 'mult'
Factorization algorithm, specified as the comma-separated pair
consisting of 'Algorithm' and
'als' (alternating least squares) or
'mult' (a multiplicative update
algorithm).
The 'als' algorithm typically is more stable and
converges in fewer iterations. Each iteration takes longer. Therefore,
the default maximum is 50, which usually gives satisfactory results in
internal testing.
The 'mult' algorithm typically has faster
iterations and requires more of them. The default maximum is 100. This
algorithm tends to be more sensitive to starting values and, therefore,
seems to benefit more from running multiple replications.
Example: 'Algorithm','mult'
Data Types: char | string
Options — Algorithm options
[] (default) | structure returned by statset
Algorithm options, specified as the comma-separated pair consisting
of 'Options' and a structure returned by the
statset function.
nnmf uses the following fields of the options
structure.
| Field | Description | Values |
|---|---|---|
Display | Level of iterative display |
|
MaxIter | Maximum number of iterations | Positive integer. The default is
50 for the
'als' algorithm and
100 for the
'mult' algorithm. Unlike in
optimization settings, reaching
MaxIter iterations is treated as
convergence. |
TolFun | Termination tolerance on the change in size of the residual | Nonnegative value. The default is
1e-4. |
TolX | Termination tolerance on the relative change in the
elements of W and
H | Nonnegative value. The default is
1e-4. |
UseParallel | Indication to compute in parallel | Logical value. The default false
indicates not to compute in parallel, and
true indicates to compute in
parallel. Computing in parallel requires a Parallel Computing Toolbox™ license. |
UseSubstreams | Type of reproducibility when computing in parallel |
For details, see Reproducibility in Parallel Statistical Computations. |
Streams | A RandStream object or cell array of such
objects |
|
Example: 'Options',statset('Display','iter','MaxIter',50)
Data Types: struct
Replicates — Number of times to repeat factorization
1 (default) | positive integer
Number of times to repeat the factorization, specified as the
comma-separated pair consisting of 'Replicates' and a
positive integer. The algorithm chooses new random starting values for
W and H at each replication,
except at the first replication if you specify 'W0'
and 'H0'. If you specify a value greater than
1, you can obtain better results by setting
Algorithm to 'mult'. See
Change Algorithm.
Example: 10
Data Types: single | double
Output Arguments
D — Root mean square residual
nonnegative scalar
Root mean square residual, returned as a nonnegative scalar.
D = norm(A - W*H,'fro')/sqrt(n*m)References
[1] Berry, Michael W., Murray Browne, Amy N. Langville, V. Paul Pauca, and Robert J. Plemmons. “Algorithms and Applications for Approximate Nonnegative Matrix Factorization.” Computational Statistics & Data Analysis 52, no. 1 (September 2007): 155–73. https://doi.org/10.1016/j.csda.2006.11.006.
Extended Capabilities
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2008a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)