Noncentral t Distribution
Definition
The most general representation of the noncentral t distribution is quite complicated. Johnson and Kotz [67] give a formula for the probability that a noncentral t variate falls in the range [–u, u].
I(x|ν,δ) is the incomplete beta function with parameters ν and δ. δ is the noncentrality parameter, and ν is the number of degrees of freedom.
Background
The noncentral t distribution is a generalization of Student's t distribution.
Student's t distribution with n – 1 degrees of freedom models the t-statistic
where is the sample mean and s is the sample standard deviation of a random sample of size n from a normal population with mean μ. If the population mean is actually μ0, then the t-statistic has a noncentral t distribution with noncentrality parameter
The noncentrality parameter is the normalized difference between μ0 and μ.
The noncentral t distribution gives the probability that a t test will correctly reject a false null hypothesis of mean μ when the population mean is actually μ0; that is, it gives the power of the t test. The power increases as the difference μ0 – μ increases, and also as the sample size n increases.
Examples
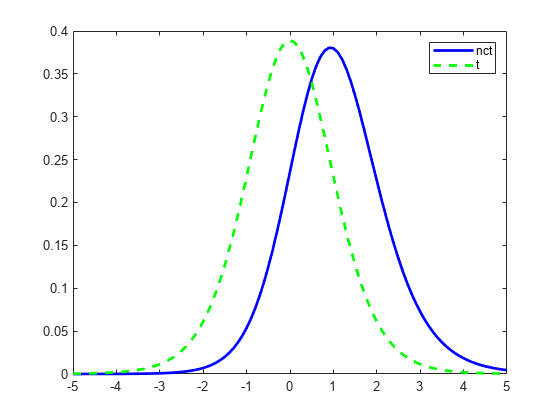
Compute Noncentral t Distribution pdf
Compute the pdf of a noncentral t distribution with degrees of freedom V = 10 and noncentrality parameter DELTA = 1. For comparison, also compute the pdf of a t distribution with the same degrees of freedom.
x = (-5:0.1:5)'; nct = nctpdf(x,10,1); t = tpdf(x,10);
Plot the pdf of the noncentral t distribution and the pdf of the t distribution on the same figure.
plot(x,nct,'b-','LineWidth',2) hold on plot(x,t,'g--','LineWidth',2) legend('nct','t')
See Also
nctcdf | nctpdf | nctinv | nctstat | nctrnd | random
