plotDiagnostics
Plot diagnostics of nonlinear regression model
Syntax
Description
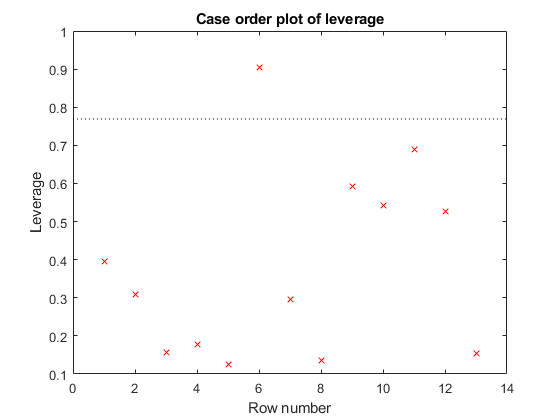
plotDiagnostics creates a plot of observation
diagnostics such as leverage or Cook's distance statistics to identify outliers and
influential observations.
plotDiagnostics( creates a
leverage plot of the nonlinear regression model (mdl)mdl)
observations. A dotted line in the plot represents the recommended threshold
values.
plotDiagnostics(___,
specifies additional options using one or more name-value arguments in addition
to any of the input argument combinations in the previous syntaxes. For example,
you can specify the marker symbol and size for the data points.Name,Value)
h = plotDiagnostics(___)h to modify the properties of a specific line or
contour after you create the plot. For a list of properties, see Line Properties and Contour Properties.
Examples
Input Arguments
Output Arguments
More About
Tips
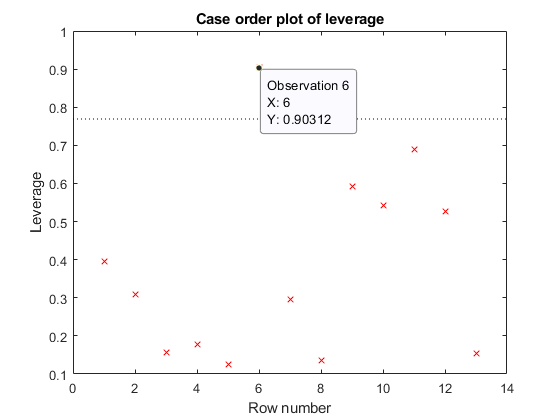
The data cursor displays the values of the selected plot point in a data tip (small text box located next to the data point). The data tip includes the x-axis and y-axis values for the selected point, along with the observation name or number.
References
[1] Neter, J., M. H. Kutner, C. J. Nachtsheim, and W. Wasserman. Applied Linear Statistical Models, Fourth Edition. Irwin, Chicago, 1996.