refcurve
Add reference curve to plot
Syntax
refcurve(p)
refcurve
refcurve(ax,p)
hcurve = refcurve(...)
Description
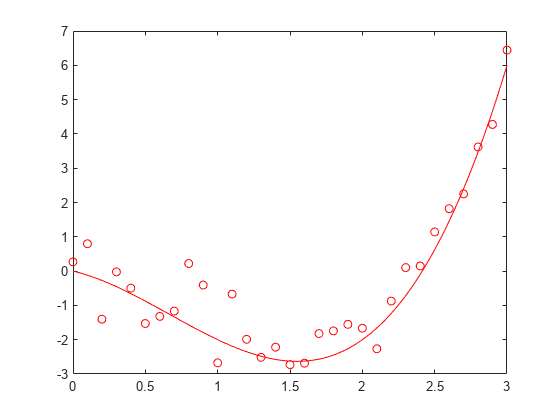
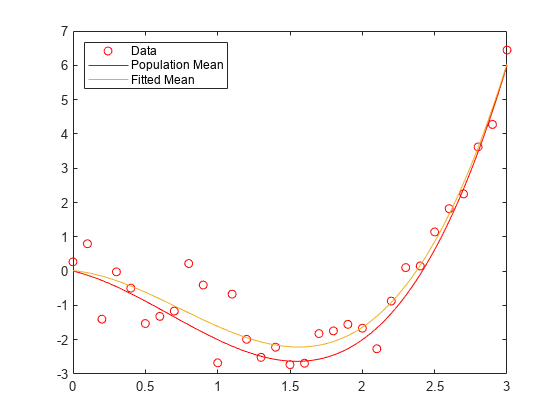
refcurve(p) adds a polynomial reference
curve with coefficients p to the current axes.
If p is a vector with n+1 elements,
the curve is:
y = p(1)*x^n + p(2)*x^(n-1) + ... + p(n)*x + p(n+1)
refcurve with no input arguments
adds a line along the x axis.
refcurve(ax,p) uses the plot axes specified in
ax, an Axes object. For more information, see
axes.
hcurve = refcurve(...) returns the handle
hcurve to the curve using any of the input
argument combinations in the previous syntaxes.
Examples
Version History
Introduced before R2006a