regstats
Regression diagnostics
Syntax
regstats(y,X,model)
stats = regstats(...)
stats = regstats(y,X,model,whichstats)
Description
regstats(y,X, performs
a multilinear regression of the responses in model)y on
the predictors in X. X is an n-by-p matrix
of p predictors at each of n observations. y is
an n-by-1 vector of observed responses.
Note
By default, regstats adds a first column
of 1s to X, corresponding to a constant term in
the model. Do not enter a column of 1s directly into X.
The optional input model controls
the regression model. By default, regstats uses
a linear additive model with a constant term. model can
be any one of the following:
'linear'— Constant and linear terms (the default)'interaction'— Constant, linear, and interaction terms'quadratic'— Constant, linear, interaction, and squared terms'purequadratic'— Constant, linear, and squared terms
Alternatively, model can be a matrix of model
terms accepted by the x2fx function.
See x2fx for a description of
this matrix and for a description of the order in which terms appear.
You can use this matrix to specify other models including ones without
a constant term.
With this syntax, the function displays a graphical user interface (GUI) with a list of diagnostic statistics, as shown in the following figure.
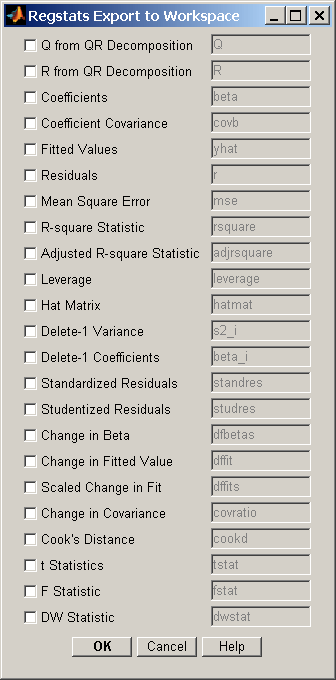
When you select check boxes corresponding to the statistics
you want to compute and click OK, regstats returns
the selected statistics to the MATLAB® workspace. The names of
the workspace variables are displayed on the right-hand side of the
interface. You can change the name of the workspace variable to any
valid MATLAB variable name.
stats = regstats(...) creates the structure stats,
whose fields contain all of the diagnostic statistics for the regression.
This syntax does not open the GUI. The fields of stats are
listed in the following table.
| Field | Description |
|---|---|
Q | Q from the QR decomposition of the design matrix |
R | R from the QR decomposition of the design matrix |
beta | Regression coefficients |
covb | Covariance of regression coefficients |
yhat | Fitted values of the response data |
r | Residuals |
mse | Mean squared error |
rsquare | R2 statistic |
adjrsquare | Adjusted R2 statistic |
leverage | Leverage |
hatmat | Hat matrix |
s2_i | Delete-1 variance |
beta_i | Delete-1 coefficients |
standres | Standardized residuals |
studres | Studentized residuals |
dfbetas | Scaled change in regression coefficients |
dffit | Change in fitted values |
dffits | Scaled change in fitted values |
covratio | Change in covariance |
cookd | Cook's distance |
tstat | t statistics and p-values for coefficients |
fstat | F statistic and p-value |
dwstat | Durbin-Watson statistic and p-value |
Note that the fields names of stats correspond
to the names of the variables returned to the MATLAB workspace
when you use the GUI. For example, stats.beta corresponds
to the variable beta that is returned when you
select Coefficients in the GUI and click OK.
stats = regstats(y,X,
returns only the statistics that you specify in model,whichstats)whichstats.
whichstats can be a single character vector such as
'leverage', a string array such as
["leverage","standres","studres"], or a cell array of character vectors such
as {'leverage','standres','studres'}. Set
whichstats to 'all' to return all of the
statistics.
Note
The F statistic is computed under the assumption that the model contains a constant term. It is not correct for models without a constant. The R2 statistic can be negative for models without a constant, which indicates that the model is not appropriate for the data.
Examples
Open the regstats GUI using data from hald.mat:
load hald regstats(heat,ingredients,'linear');
Select Fitted Values and Residuals in the GUI:

Click OK to export the fitted values
and residuals to the MATLAB workspace in variables named yhat and r,
respectively.
You can create the same variables using the stats output,
without opening the GUI:
whichstats = {'yhat','r'};
stats = regstats(heat,ingredients,'linear',whichstats);
yhat = stats.yhat;
r = stats.r;
Tips
regstatstreatsNaNvalues inXoryas missing values.regstatsomits observations with missing values from the regression fit.
References
[1] Belsley, D. A., E. Kuh, and R. E. Welsch. Regression Diagnostics. Hoboken, NJ: John Wiley & Sons, Inc., 1980.
[2] Chatterjee, S., and A. S. Hadi. “Influential Observations, High Leverage Points, and Outliers in Linear Regression.” Statistical Science. Vol. 1, 1986, pp. 379–416.
[3] Cook, R. D., and S. Weisberg. Residuals and Influence in Regression. New York: Chapman & Hall/CRC Press, 1983.
[4] Goodall, C. R. “Computation Using the QR Decomposition.” Handbook in Statistics. Vol. 9, Amsterdam: Elsevier/North-Holland, 1993.
Version History
Introduced before R2006a
