predict
Compute predicted values given predictor values
Description
ypred = predict(rm,tnew,Name,Value)rm with
additional options specified by one or more Name,Value pair
arguments.
For example, you can specify the within-subjects design matrix.
Examples
Predict Response Values
Load the sample data.
load fisheririsThe column vector species consists of iris flowers of three different species: setosa, versicolor, and virginica. The double matrix meas consists of four types of measurements on the flowers: the length and width of sepals and petals in centimeters, respectively.
Store the data in a table array.
t = table(species,meas(:,1),meas(:,2),meas(:,3),meas(:,4), ... 'VariableNames',{'species','meas1','meas2','meas3','meas4'}); Meas = dataset([1 2 3 4]','VarNames',{'Measurements'});
Fit a repeated measures model, where the measurements are the responses and the species is the predictor variable.
rm = fitrm(t,'meas1-meas4~species','WithinDesign',Meas);
Predict responses for the three species.
Y = predict(rm,t([1 51 101],:))
Y = 3×4
5.0060 3.4280 1.4620 0.2460
5.9360 2.7700 4.2600 1.3260
6.5880 2.9740 5.5520 2.0260
Predict Response Values and Plot Predictions
Load the sample data.
load longitudinalDataThe matrix Y contains response data for 16 individuals. The response is the blood level of a drug measured at five time points (time = 0, 2, 4, 6, and 8). Each row of Y corresponds to an individual, and each column corresponds to a time point. The first eight subjects are female, and the second eight subjects are male. This is simulated data.
Define a variable that stores gender information.
Gender = ['F' 'F' 'F' 'F' 'F' 'F' 'F' 'F' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M']';
Store the data in a proper table array format to perform repeated measures analysis.
t = table(Gender,Y(:,1),Y(:,2),Y(:,3),Y(:,4),Y(:,5), ... 'VariableNames',{'Gender','t0','t2','t4','t6','t8'});
Define the within-subjects variable.
Time = [0 2 4 6 8]';
Fit a repeated measures model, where the blood levels are the responses and gender is the predictor variable.
rm = fitrm(t,'t0-t8 ~ Gender','WithinDesign',Time);
Predict the responses at intermediate times.
time = linspace(0,8)'; Y = predict(rm,t([1 5 8 12],:), ... 'WithinModel','orthogonalcontrasts','WithinDesign',time);
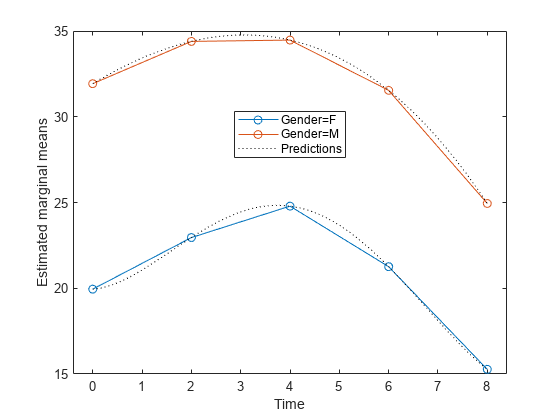
Plot the predictions along with the estimated marginal means.
plotprofile(rm,'Time','Group',{'Gender'}) hold on; plot(time,Y,'Color','k','LineStyle',':'); legend('Gender=F','Gender=M','Predictions') hold off
Compute and Plot Confidence Intervals
Load the sample data.
load longitudinalDataThe matrix Y contains response data for 16 individuals. The response is the blood level of a drug measured at five time points (time = 0, 2, 4, 6, and 8). Each row of Y corresponds to an individual, and each column corresponds to a time point. The first eight subjects are female, and the second eight subjects are male. This is simulated data.
Define a variable that stores gender information.
Gender = ['F' 'F' 'F' 'F' 'F' 'F' 'F' 'F' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M']';
Store the data in a proper table array format to perform repeated measures analysis.
t = table(Gender,Y(:,1),Y(:,2),Y(:,3),Y(:,4),Y(:,5), ... 'VariableNames',{'Gender','t0','t2','t4','t6','t8'});
Define the within-subjects variable.
Time = [0 2 4 6 8]';
Fit a repeated measures model, where the blood levels are the responses and gender is the predictor variable.
rm = fitrm(t,'t0-t8 ~ Gender','WithinDesign',Time);
Predict the responses at intermediate times.
time = linspace(0,8)'; [ypred,ypredci] = predict(rm,t([1 5 8 12],:), ... 'WithinModel','orthogonalcontrasts','WithinDesign',time);
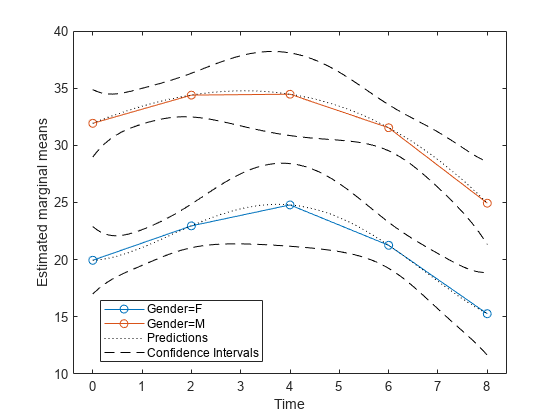
Plot the predictions and the confidence intervals for predictions along with the estimated marginal means.
p1 = plotprofile(rm,'Time','Group',{'Gender'}); hold on; p2 = plot(time,ypred,'Color','k','LineStyle',':'); p3 = plot(time,ypredci(:,:,1),'k--'); p4 = plot(time,ypredci(:,:,2),'k--'); legend([p1;p2(1);p3(1)],'Gender=F','Gender=M','Predictions','Confidence Intervals') hold off
Input Arguments
rm — Repeated measures model
RepeatedMeasuresModel object
Repeated measures model, returned as a RepeatedMeasuresModel object.
For properties and methods of this object, see RepeatedMeasuresModel.
tnew — New data
table used to create rm (default) | table
New data including the values of the response variables and
the between-subject factors used as predictors in the repeated measures
model, rm, specified as a table. tnew must
contain all of the between-subject factors used to create rm.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: ypred = predict(rm,tnew,'alpha',0.01)
Alpha — Significance level
0.05 (default) | scalar value in the range of 0 through 1
Significance level of the confidence intervals for the predicted
values, specified as the comma-separated pair consisting of
'alpha' and a scalar value in the range of 0 to
1. The confidence level is 100*(1–alpha)%.
Example: 'alpha',0.01
Data Types: double | single
WithinModel — Model for within-subject factors
'separatemeans' | 'orthogonalcontrats' | character vector | string scalar
Model for the within-subject factors, specified as the comma-separated
pair consisting of 'WithinModel' and one of the
following:
'separatemeans'— Compute a separate mean for each group.'orthogonalcontrasts'— Valid when the within-subject design consists of a single numeric factor T. This specifies a model consisting of orthogonal polynomials up to order T(r-1), where r is the number of repeated measures.A character vector or string scalar that defines a model specification in the within-subject factors.
Example: 'WithinModel','orthogonalcontrasts'
Data Types: char | string
WithinDesign — Design for within-subject factors
vector | matrix | table
Design for within-subject factors, specified as the comma-separated
pair consisting of 'WithinDesign' and a vector,
matrix, or a table. It provides the values of the within-subject factors
in the same form as the RM.WithinDesign property.
Example: 'WithinDesign','Time'
Data Types: single | double | table
Output Arguments
yci — Confidence intervals for predicted values
n-by-r-by-2 matrix
Confidence intervals for predicted values from the repeated
measures model rm, returned as an n-by-r-by-2
matrix.
These are nonsimultaneous intervals for predicting the mean
response at the specified predictor values. For predicted value ypred(i,j),
the lower limit of the interval is yci(i,j,1) and
the upper limit is yci(i,j,2).
Version History
Introduced in R2014a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)