Equation Solving
You can solve algebraic equations, differential equations, and differential algebraic equations (DAEs).
Solve algebraic equations to get either exact
analytic solutions or high-precision numeric solutions. For analytic solutions,
use solve, and for numerical solutions, use
vpasolve. For solving linear equations, use
linsolve. These solver functions have the flexibility to
handle complicated problems. See Troubleshoot Equation Solutions from solve Function.
Solve differential equations by using
dsolve. Create these
differential equations by using symbolic functions. See Create Symbolic Functions.
Solve differential algebraic equations (DAEs)
by first reducing their differential index to 1 or
0 using Symbolic Math Toolbox™ functions, and then using MATLAB® solvers, such as ode15i,
ode15s, or ode23t. See Solve Differential Algebraic Equations (DAEs).
Live Editor Tasks
| Solve Symbolic Equation | Find analytic solutions of symbolic equations in Live Editor (Since R2020a) |
Functions
Topics
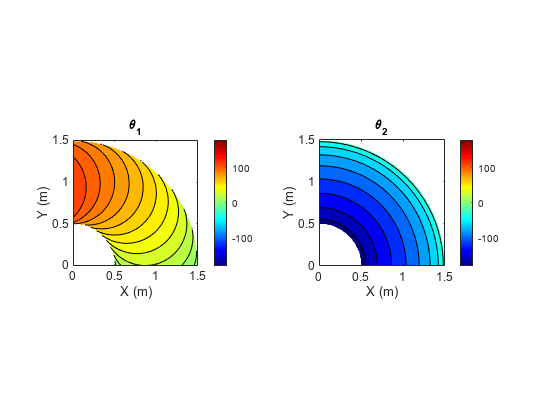
- Solve Algebraic Equations
Solve equations analytically, return full solutions, and visualize results.
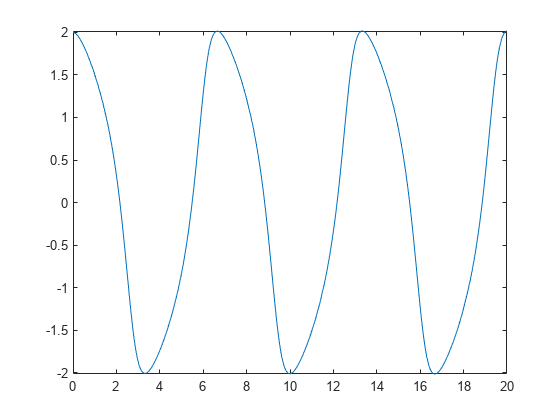
- Solve Differential Equation
Solve a differential equation analytically by using the
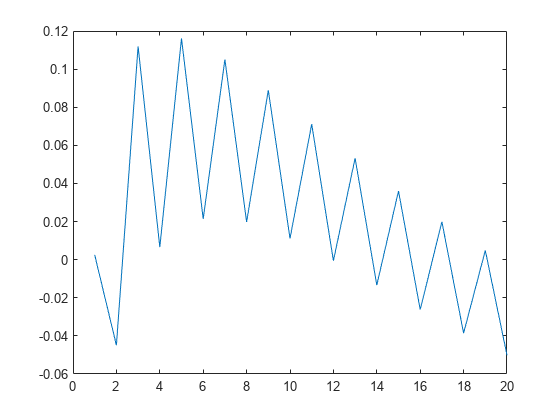
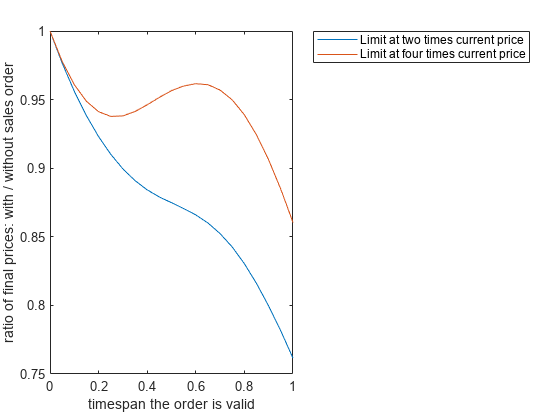
dsolvefunction, with or without initial conditions. - Solve Differential Algebraic Equations (DAEs)
This example show how to solve differential algebraic equations (DAEs) by using MATLAB® and Symbolic Math Toolbox™.