Solve Algebraic Equations
Symbolic Math Toolbox™ offers both symbolic and numeric equation
solvers. This topic shows you how to solve an equation symbolically
using the symbolic solver solve. To compare symbolic
and numeric solvers, see Select Numeric or Symbolic Solver.
Solve an Equation
If eqn is an equation, solve(eqn,
x) solves eqn for the symbolic variable x.
Use the == operator to specify the familiar
quadratic equation and solve it using solve.
syms a b c x eqn = a*x^2 + b*x + c == 0; solx = solve(eqn, x)
solx = -(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a)
solx is a symbolic vector containing the
two solutions of the quadratic equation. If the input eqn is
an expression and not an equation, solve solves
the equation eqn == 0.
To solve for a variable other than x, specify
that variable instead. For example, solve eqn for b.
solb = solve(eqn, b)
solb = -(a*x^2 + c)/x
If you do not specify a variable, solve uses symvar to
select the variable to solve for. For example, solve(eqn) solves eqn for x.
Return the Full Solution to an Equation
solve does not automatically return all
solutions of an equation. Solve the equation cos(x) == -sin(x).
The solve function returns one of many solutions.
syms x solx = solve(cos(x) == -sin(x), x)
solx = -pi/4
To return all solutions along with the parameters in the solution
and the conditions on the solution, set the ReturnConditions option
to true. Solve the same equation for the full
solution. Provide three output variables: for the solution to x,
for the parameters in the solution, and for the conditions on the
solution.
syms x [solx, param, cond] = solve(cos(x) == -sin(x), x, 'ReturnConditions', true)
solx = pi*k - pi/4 param = k cond = in(k, 'integer')
solx contains the solution for x,
which is pi*k - pi/4. The param variable
specifies the parameter in the solution, which is k.
The cond variable specifies the condition in(k,
'integer') on the solution, which means k must
be an integer. Thus, solve returns a periodic
solution starting at pi/4 which repeats at intervals
of pi*k, where k is an integer.
Work with the Full Solution, Parameters, and Conditions Returned by solve
You can use the solutions, parameters, and conditions returned
by solve to find solutions within an interval
or under additional conditions.
To find values of x in the interval -2*pi<x<2*pi,
solve solx for k within that
interval under the condition cond. Assume the condition cond using assume.
assume(cond) solk = solve(-2*pi<solx, solx<2*pi, param)
solk = -1 0 1 2
To find values of x corresponding to these
values of k, use subs to substitute
for k in solx.
xvalues = subs(solx, solk)
xvalues =
-(5*pi)/4
-pi/4
(3*pi)/4
(7*pi)/4To convert these symbolic values into numeric values for use
in numeric calculations, use vpa.
xvalues = vpa(xvalues)
xvalues = -3.9269908169872415480783042290994 -0.78539816339744830961566084581988 2.3561944901923449288469825374596 5.4977871437821381673096259207391
Visualize and Plot Solutions Returned by solve
The previous sections used solve to solve
the equation cos(x) == -sin(x). The solution to
this equation can be visualized using plotting functions such as fplot and scatter.
Plot both sides of equation cos(x) == -sin(x).
fplot(cos(x)) hold on grid on fplot(-sin(x)) title('Both sides of equation cos(x) = -sin(x)') legend('cos(x)','-sin(x)','Location','best','AutoUpdate','off')
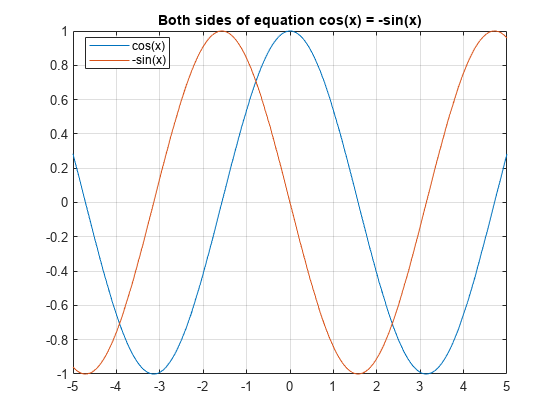
Calculate the values of the functions at the values of x,
and superimpose the solutions as points using scatter.
yvalues = cos(xvalues)
yvalues =
scatter(xvalues, yvalues)
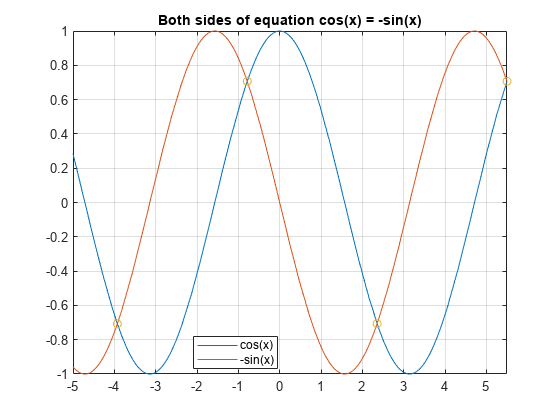
As expected, the solutions appear at the intersection of the two plots.
Simplify Complicated Results and Improve Performance
If results look complicated, solve is stuck,
or if you want to improve performance, see, Troubleshoot Equation Solutions from solve Function.
