Taylor Series
The statements
syms x f = 1/(5 + 4*cos(x)); T = taylor(f, 'Order', 8)
return
T = (49*x^6)/131220 + (5*x^4)/1458 + (2*x^2)/81 + 1/9
which is all the terms up to, but not including, order eight in the Taylor series for f(x):
Technically, T is a Maclaurin series, since its expansion point is a = 0.
These commands
syms x g = exp(x*sin(x)); t = taylor(g, 'ExpansionPoint', 2, 'Order', 12);
generate the first 12 nonzero terms of the Taylor series for g about
x = 2.
t is a large expression; enter
size(char(t))
ans =
1 99791to find that t has about 100,000 characters in its printed form. In
order to proceed with using t, first simplify its presentation:
t = simplify(t); size(char(t))
ans =
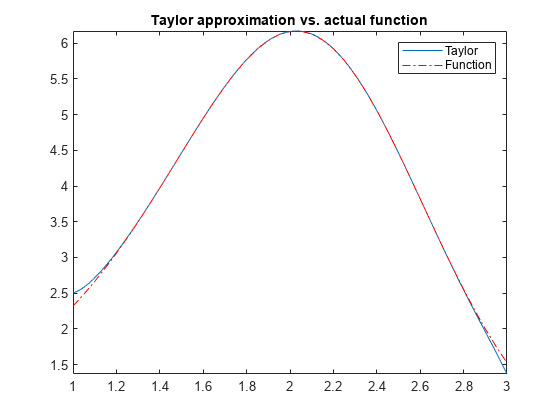
1 6988Next, plot these functions together to see how well this Taylor approximation compares to
the actual function g:
xd = 1:0.05:3; yd = subs(g,x,xd); fplot(t, [1, 3]) hold on plot(xd, yd, 'r-.') title('Taylor approximation vs. actual function') legend('Taylor','Function')
Special thanks is given to Professor Gunnar Bäckstrøm of UMEA in Sweden for this example.
