Wavelet Analysis of Physiologic Signals
This example shows how to use wavelets to analyze physiologic signals.
Physiologic signals are frequently nonstationary meaning that their frequency content changes over time. In many applications, these changes are the events of interest.
Wavelets decompose signals into time-varying frequency (scale) components. Because signal features are often localized in time and frequency, analysis and estimation are easier when working with sparser (reduced) representations.
This example presents a few illustrative cases where the ability of wavelets to provide a local time-frequency analysis of signals is beneficial.
R Wave Detection in the Electrocardiogram with MODWT
The QRS complex consists of three deflections in the electrocardiogram (ECG) waveform. The QRS complex reflects the depolarization of the right and left ventricles and is the most prominent feature of the human ECG.
Load and plot an ECG waveform where the R peaks of the QRS complex have been annotated by two or more cardiologists. The ECG data and annotations are taken from the MIT-BIH Arrhythmia Database. The data are sampled at 360 Hz.
load mit200 figure plot(tm,ecgsig) hold on plot(tm(ann),ecgsig(ann),'ro') xlabel('Seconds') ylabel('Amplitude') title('Subject - MIT-BIH 200')

You can use wavelets to build an automatic QRS detector for use in applications like R-R interval estimation.
There are two keys for using wavelets as general feature detectors:
The wavelet transform separates signal components into different frequency bands enabling a sparser representation of the signal.
You can often find a wavelet which resembles the feature you are trying to detect.
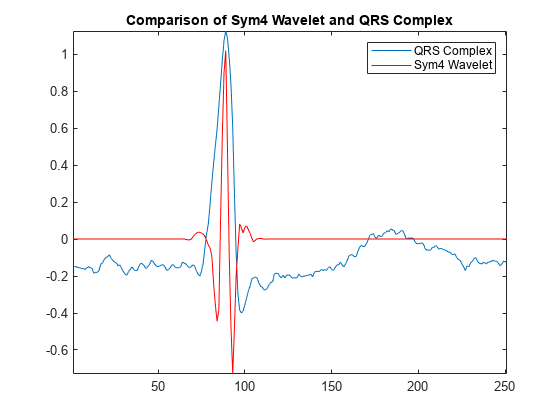
The 'sym4' wavelet resembles the QRS complex, which makes it a good choice for QRS detection. To illustrate this more clearly, extract a QRS complex and plot the result with a dilated and translated 'sym4' wavelet for comparison.
qrsEx = ecgsig(4560:4810); fb = dwtfilterbank('Wavelet','sym4','SignalLength',numel(qrsEx),'Level',3); psi = wavelets(fb); figure plot(qrsEx) hold on plot(-2*circshift(psi(3,:),[0 -38]),'r') axis tight legend('QRS Complex','Sym4 Wavelet') title('Comparison of Sym4 Wavelet and QRS Complex') hold off
Use the maximal overlap discrete wavelet transform (MODWT) to enhance the R peaks in the ECG waveform. The MODWT is an undecimated wavelet transform, which handles arbitrary sample sizes.
First, decompose the ECG waveform down to level 5 using the default 'sym4' wavelet. Then, reconstruct a frequency-localized version of the ECG waveform using only the wavelet coefficients at scales 4 and 5. The scales correspond to the following approximate frequency bands.
Scale 4 -- [11.25, 22.5) Hz
Scale 5 -- [5.625, 11.25) Hz.
This covers the passband shown to maximize QRS energy.
wt = modwt(ecgsig,5);
wtrec = zeros(size(wt));
wtrec(4:5,:) = wt(4:5,:);
y = imodwt(wtrec,'sym4');Use the squared absolute values of the signal approximation built from the wavelet coefficients and employ a peak finding algorithm to identify the R peaks.
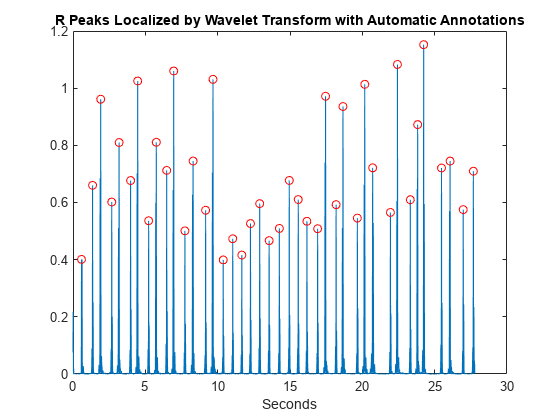
If you have Signal Processing Toolbox™, you can use findpeaks to locate the peaks. Plot the R-peak waveform obtained with the wavelet transform annotated with the automatically-detected peak locations.
y = abs(y).^2; [qrspeaks,locs] = findpeaks(y,tm,'MinPeakHeight',0.35,... 'MinPeakDistance',0.150); figure plot(tm,y) hold on plot(locs,qrspeaks,'ro') xlabel('Seconds') title('R Peaks Localized by Wavelet Transform with Automatic Annotations')
Add the expert annotations to the R-peak waveform. Automatic peak detection times are considered accurate if within 150 msec of the true peak ( msec).
plot(tm(ann),y(ann),'k*') title('R peaks Localized by Wavelet Transform with Expert Annotations')
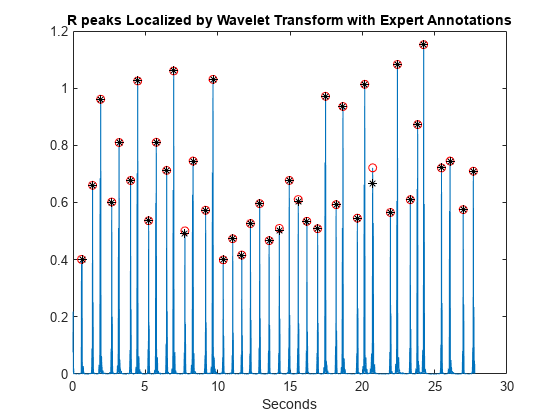
At the command line, you can compare the values of tm(ann) and locs, which are the expert times and automatic peak detection times respectively. Enhancing the R peaks with the wavelet transform results in a hit rate of 100% and no false positives. The calculated heart rate using the wavelet transform is 88.60 beats/minute compared to 88.72 beats/minute for the annotated waveform.
If you try to work on the square magnitudes of the original data, you find the capability of the wavelet transform to isolate the R peaks makes the detection problem much easier. Working on the raw data can cause misidentifications such as when the squared S-wave peak exceeds the R-wave peak around 10.4 seconds.
figure plot(tm,ecgsig,'k--') hold on plot(tm,y,'r','linewidth',1.5) plot(tm,abs(ecgsig).^2,'b') plot(tm(ann),ecgsig(ann),'ro','markerfacecolor',[1 0 0]) set(gca,'xlim',[10.2 12]) legend('Raw Data','Wavelet Reconstruction','Raw Data Squared', ... 'Location','SouthEast') xlabel('Seconds')
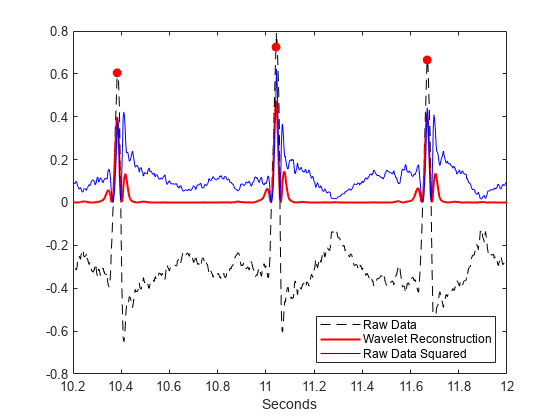
Using findpeaks on the squared magnitudes of the raw data results in twelve false positives.
[qrspeaks,locs] = findpeaks(ecgsig.^2,tm,'MinPeakHeight',0.35,... 'MinPeakDistance',0.150);
In addition to switches in polarity of the R peaks, the ECG is often corrupted by noise.
load mit203 figure plot(tm,ecgsig) hold on plot(tm(ann),ecgsig(ann),'ro') xlabel('Seconds') ylabel('Amplitude') title('Subject - MIT-BIH 203 with Expert Annotations')

Use the MODWT to isolate the R peaks. Use findpeaks to determine the peak locations. Plot the R-peak waveform along with the expert and automatic annotations.
wt = modwt(ecgsig,5); wtrec = zeros(size(wt)); wtrec(4:5,:) = wt(4:5,:); y = imodwt(wtrec,'sym4'); y = abs(y).^2; [qrspeaks,locs] = findpeaks(y,tm,'MinPeakHeight',0.1,... 'MinPeakDistance',0.150); figure plot(tm,y) title('R-Waves Localized by Wavelet Transform') hold on hwav = plot(locs,qrspeaks,'ro'); hexp = plot(tm(ann),y(ann),'k*'); xlabel('Seconds') legend([hwav hexp],'Automatic','Expert','Location','NorthEast')
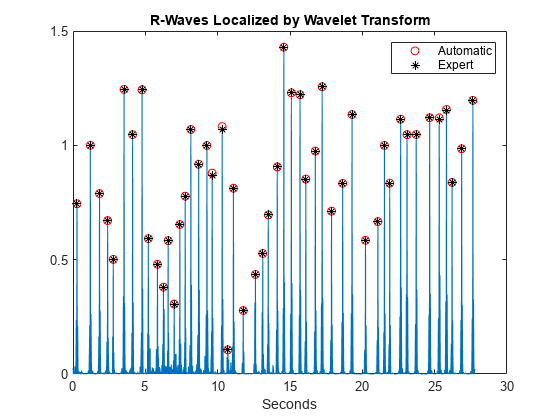
The hit rate is again 100% with zero false alarms.
The previous examples used a very simple wavelet QRS detector based on a signal approximation constructed from modwt. The goal was to demonstrate the ability of the wavelet transform to isolate signal components, not to build the most robust wavelet-transform-based QRS detector. It is possible, for example, to exploit the fact that the wavelet transform provides a multiscale analysis of the signal to enhance peak detection. Examine the scale 4 and 5 magnitude-squared wavelet details plotted along with R peak times as annotated by the experts. The level-4 details are shifted for visualization.
ecgmra = modwtmra(wt); figure plot(tm,ecgmra(5,:).^2,'b') hold on plot(tm,ecgmra(4,:).^2+0.6,'b') set(gca,'xlim',[14.3 25.5]) timemarks = repelem(tm(ann),2); N = numel(timemarks); markerlines = reshape(repmat([0;1],1,N/2),N,1); h = stem(timemarks,markerlines,'k--'); h.Marker = 'none'; set(gca,'ytick',[0.1 0.6]); set(gca,'yticklabels',{'D5','D4'}) xlabel('Seconds') title('Magnitude-Squared Level 4 and 5 Details')
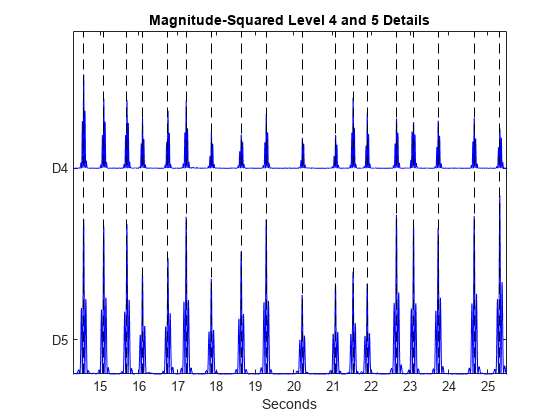
You see that peaks in the level 4 and level 5 details tend to co-occur. A more advanced wavelet peak-finding algorithm could exploit this by using information from multiple scales simultaneously.
Time-Varying Wavelet Coherence Analysis of Brain Dynamics
Fourier-domain coherence is a well-established technique for measuring the linear correlation between two stationary processes as a function of frequency on a scale from 0 to 1. Because wavelets provide local information about data in time and scale (frequency), wavelet-based coherence allows you to measure time-varying correlation as a function of frequency. In other words, a coherence measure suitable for nonstationary processes.
To illustrate this, examine near-infrared spectroscopy (NIRS) data obtained in two human subjects. NIRS measures brain activity by exploiting the different absorption characteristics of oxygenated and deoxygenated hemoglobin. The data is taken from Cui, Bryant, & Reiss (2012) and was kindly provided by the authors for this example. The recording site was the superior frontal cortex for both subjects. The data is sampled at 10 Hz.
In the experiment, the subjects alternatively cooperated and competed on a task. The period of the task was seven seconds.
load NIRSData figure plot(tm,[NIRSData(:,1) NIRSData(:,2)]) legend('Subject 1','Subject 2','Location','NorthWest') xlabel('Seconds') title('NIRS Data') grid on
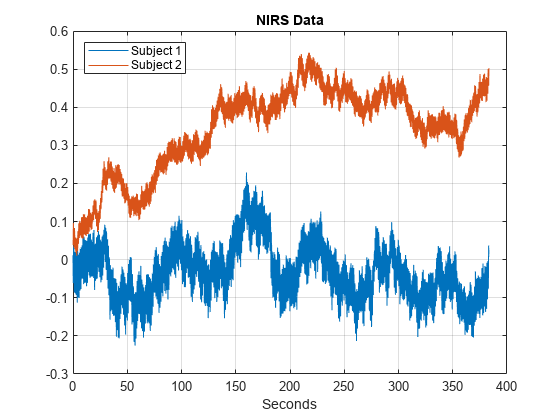
Examining the time-domain data, it is not clear what oscillations are present in the individual time series, or what oscillations are common to both data sets. Use wavelet analysis to answer both questions.
cwt(NIRSData(:,1),10,'bump')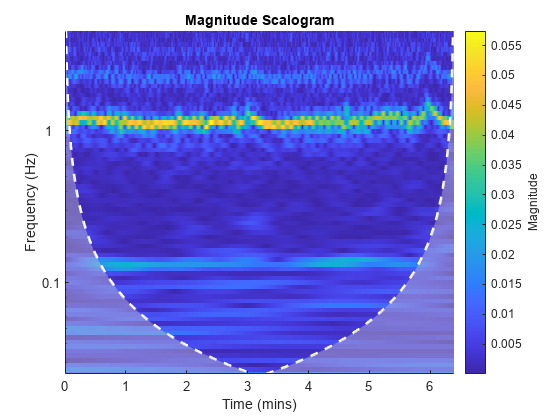
figure
cwt(NIRSData(:,2),10,'bump')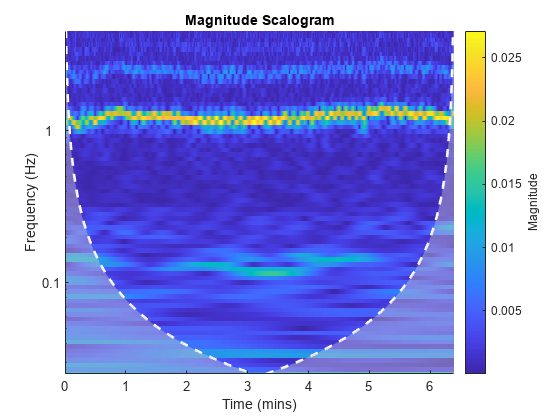
The CWT analyses reveal strong frequency-modulated oscillations in both datasets around 1 Hz. These are due to the cardiac cycles in the two subjects. Additionally, there appears to be a weaker oscillation in both datasets around 0.15 Hz. This activity is stronger and more consistent in subject 1 than subject 2. Wavelet coherence can enhance the detection of weak oscillations that are jointly present in two time series.
[wcoh,~,F] = wcoherence(NIRSData(:,1),NIRSData(:,2),10); figure surf(tm,F,abs(wcoh).^2); view(0,90) shading interp axis tight hc = colorbar; hc.Label.String = 'Coherence'; title('Wavelet Coherence') xlabel('Seconds') ylabel('Hz') ylim([0 2.5]) set(gca,'ytick',[0.15 1.2 2])
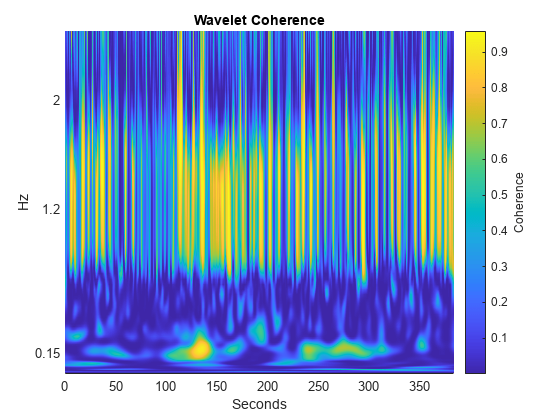
In the wavelet coherence, there is a strong correlation around 0.15 Hz. This is in the frequency band corresponding to the experimental task and represents task-related coherent oscillations in brain activity in the two subjects. Add time markers which indicate two task periods to the plot. The period between the tasks is a rest period.
taskbd = [245 1702 2065 3474]; tvec = repelem(tm(taskbd),2); yvec = [0 max(F)]'; yvec = reshape(repmat(yvec,1,4),8,1); hold on stemPlot = stem(tvec,yvec,'w--','linewidth',2); stemPlot.Marker = 'none';
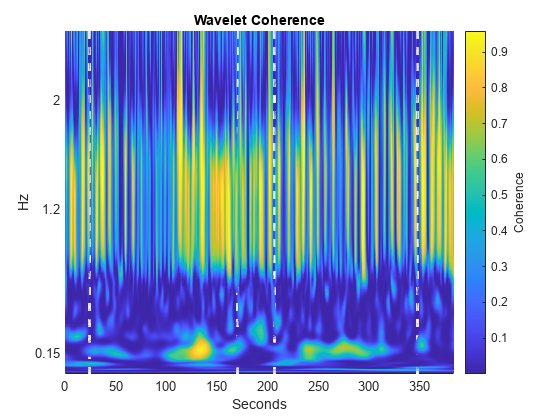
This example used cwt to obtain and plot a time-frequency analysis of the individual NIRS time series. The example also used wcoherence to obtain the wavelet coherence of the two time series. The use of wavelet coherence often enables you to detect coherent oscillatory behavior in two time series which may be fairly weak in each individual series. Consult Cui, Bryant, & Reiss (2012) for a more detailed wavelet-coherence analysis of this data.
Time-Frequency Analysis of Otoacoustic Emission Data with the CWT
Otoacoustic emissions (OAEs) are narrowband oscillatory signals emitted by the cochlea (inner ear) and their presence is indicative of normal hearing. Load and plot some example OAE data. The data are sampled at 20 kHz.
load dpoae figure plot(t.*1000,dpoaets) xlabel('Milliseconds') ylabel('Amplitude')
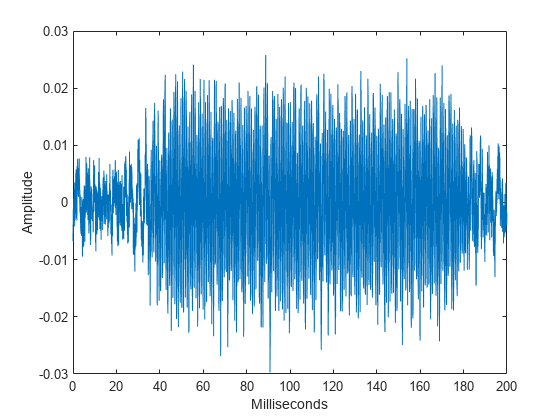
The emission was evoked by a stimulus beginning at 25 milliseconds and ending at 175 milliseconds. Based on the experimental parameters, the emission frequency should be 1230 Hz. Obtain and plot the CWT as a function of time and frequency. Use the default analytic Morse wavelet with 16 voices per octave. Use the helper function helperCWTTimeFreqPlot to plot the CWT. The helper function is in the same folder as this example.
[dpoaeCWT,f] = cwt(dpoaets,2e4,'VoicesPerOctave',16); helperCWTTimeFreqPlot(dpoaeCWT,t.*1000,f,... 'surf','CWT of OAE','milliseconds','Hz')
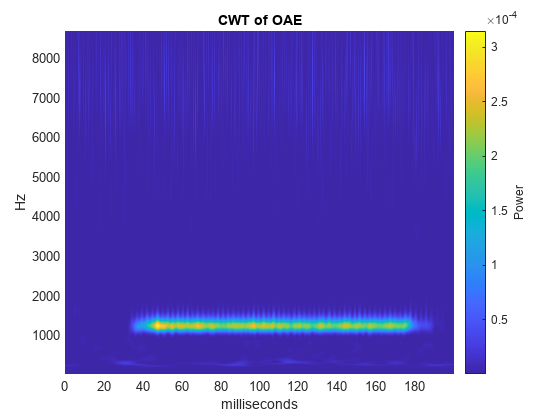
You can investigate the time evolution of the OAE by finding the CWT coefficients closest in frequency to 1230 Hz and examining their magnitudes as a function of time. Plot the magnitudes along with time markers designating the beginning and end of the evoking stimulus.
[~,idx1230] = min(abs(f-1230)); cfsOAE = dpoaeCWT(idx1230,:); plot(t.*1000,abs(cfsOAE)) hold on AX = gca; plot([25 25],[AX.YLim(1) AX.YLim(2)],'r') plot([175 175],[AX.YLim(1) AX.YLim(2)],'r') xlabel('msec') title('CWT Coefficient Magnitudes')
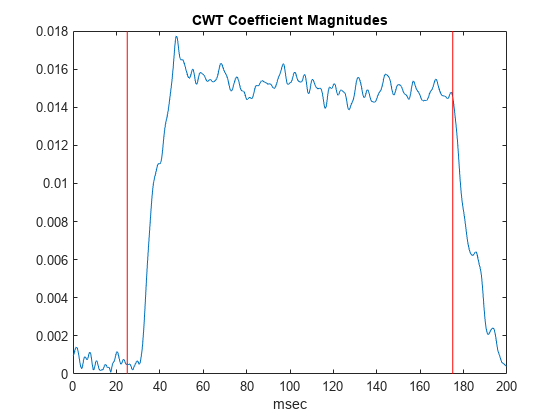
There is some delay between the onset of the evoking stimulus and the OAE. Once the evoking stimulus is terminated, the OAE immediately begins to decay in magnitude.
Another way to isolate the emission is to use the inverse CWT to reconstruct a frequency-localized approximation in the time domain.
Construct a frequency-localized emission approximation by extracting the CWT coefficients corresponding to frequencies between 1150 and 1350 Hz. Use these coefficients and invert the CWT. Plot the original data along with the reconstruction and markers indicating the beginning and end of the evoking stimulus.
frange = [1150 1350]; xrec = icwt(dpoaeCWT,[],f,frange); figure plot(t.*1000,dpoaets) hold on plot(t.*1000,xrec,'r') AX = gca; ylimits = AX.YLim; plot([25 25],ylimits,'k') plot([175 175],ylimits,'k') grid on xlabel('Milliseconds') ylabel('Amplitude') title('Frequency-Localized Reconstruction of Emission')
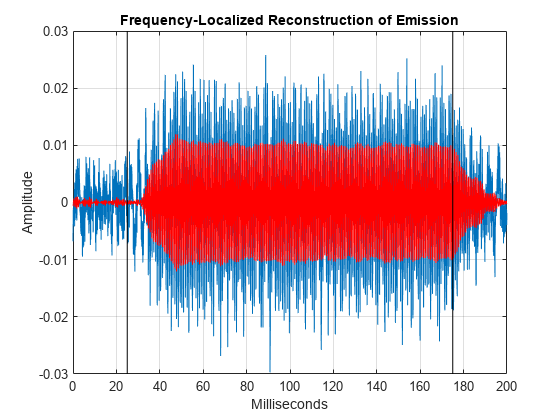
In the time-domain data, you clearly see how the emission ramps on and off at the application and termination of the evoking stimulus.
It is important to note that even though a range of frequencies were selected for the reconstruction, the analytic wavelet transform actually encodes the exact frequency of the emission. To demonstrate this, take the Fourier transform of the emission approximation reconstructed from the analytic CWT.
xdft = fft(xrec); freq = 0:2e4/numel(xrec):1e4; xdft = xdft(1:numel(xrec)/2+1); figure plot(freq,abs(xdft)) xlabel('Hz') ylabel('Magnitude') title('Fourier Transform of CWT-Based Signal Approximation')
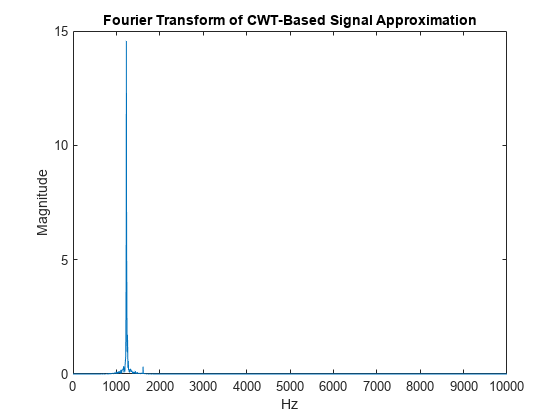
[~,maxidx] = max(abs(xdft));
fprintf('The frequency is %4.2f Hz\n',freq(maxidx))The frequency is 1230.00 Hz
This example used cwt to obtain a time-frequency analysis of the OAE data and icwt to obtain a frequency-localized approximation to the signal.
References
Cui, X., Bryant, D.M., and Reiss. A.L. "NIRS-Based hyperscanning reveals increased interpersonal coherence in superior frontal cortex during cooperation", Neuroimage, 59(3), 2430-2437, 2012.
Goldberger AL, Amaral LAN, Glass L, Hausdorff JM, Ivanov PCh, Mark RG, Mietus JE, Moody GB, Peng C-K, Stanley HE. "PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals." Circulation 101(23):e215-e220, 2000. http://circ.ahajournals.org/cgi/content/full/101/23/e215
Mallat, S. "A Wavelet Tour of Signal Processing: The Sparse Way", Academic Press, 2009.
Moody, G.B. "Evaluating ECG Analyzers". http://www.physionet.org/physiotools/wfdb/doc/wag-src/eval0.tex
Moody GB, Mark RG. "The impact of the MIT-BIH Arrhythmia Database." IEEE Eng in Med and Biol 20(3):45-50 (May-June 2001).
