Critically-Sampled Wavelet Reconstruction
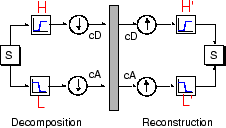
We've learned how the discrete wavelet transform can be used to analyze, or decompose, signals and images. This process is called decomposition or analysis. The other half of the story is how those components can be assembled back into the original signal without loss of information. This process is called reconstruction, or synthesis. The mathematical manipulation that effects synthesis is called the inverse discrete wavelet transform (IDWT).
To synthesize a signal using Wavelet Toolbox™ software, we reconstruct it from the wavelet coefficients.
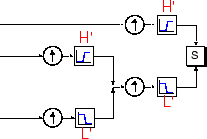
Where wavelet analysis involves filtering and downsampling, the wavelet reconstruction process consists of upsampling and filtering. Upsampling is the process of lengthening a signal component by inserting zeros between samples.
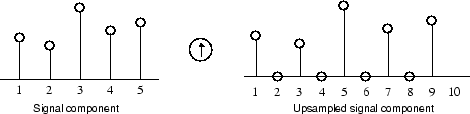
The toolbox includes commands, like idwt and waverec, that perform single-level or
multilevel reconstruction, respectively, on the components of 1-D signals. These commands have
their 2-D and 3-D analogs, idwt2, waverec2, idwt3, and waverec3.
Reconstruction Filters
The filtering part of the reconstruction process also bears some discussion, because it is the choice of filters that is crucial in achieving perfect reconstruction of the original signal.
The downsampling of the signal components performed during the decomposition phase introduces a distortion called aliasing. It turns out that by carefully choosing filters for the decomposition and reconstruction phases that are closely related (but not identical), we can “cancel out” the effects of aliasing.
A technical discussion of how to design these filters is available on page 347 of the
book Wavelets and Filter Banks, by Strang and Nguyen. The low- and
high-pass decomposition filters (L and H), together
with their associated reconstruction filters (L' and
H'), form a system of what is called quadrature mirror filters:
Reconstructing Approximations and Details
We have seen that it is possible to reconstruct our original signal from the coefficients of the approximations and details.
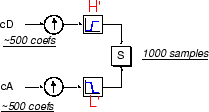
It is also possible to reconstruct the approximations and details themselves from their
coefficient vectors. As an example, let's consider how we would reconstruct the first-level
approximation A1 from the coefficient vector
cA1.
We pass the coefficient vector cA1 through the same process we used
to reconstruct the original signal. However, instead of combining it with the level-one
detail cD1, we feed in a vector of zeros in place of the detail
coefficients vector:
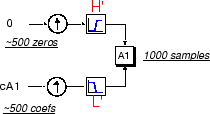
The process yields a reconstructed approximation
A1, which has the same length as the original signal S
and which is a real approximation of it.
Similarly, we can reconstruct the first-level detail D1, using the
analogous process:
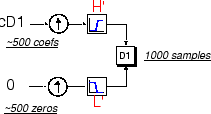
The reconstructed details and approximations are true constituents of the original signal. In fact, we find when we combine them that
A1 + D1 = S.
Note that the coefficient vectors cA1 and cD1
— because they were produced by downsampling and are only half the length of the
original signal — cannot directly be combined to reproduce the signal. It
is necessary to reconstruct the approximations and details before combining
them.
Extending this technique to the components of a multilevel analysis, we find that similar relationships hold for all the reconstructed signal constituents. That is, there are several ways to reassemble the original signal:
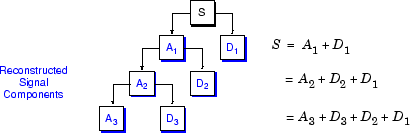
Wavelets From Conjugate Mirror Filters
In the section Reconstruction Filters, we spoke of the importance of choosing the right filters. In fact, the choice of filters not only determines whether perfect reconstruction is possible, it also determines the shape of the wavelet we use to perform the analysis.
To construct a wavelet of some practical utility, you seldom start by drawing a waveform. Instead, it usually makes more sense to design the appropriate quadrature mirror filters, and then use them to create the waveform. Let's see how this is done by focusing on an example.
Consider the low-pass reconstruction filter (L') for the
db2 wavelet.
The filter coefficients can be obtained from the dbaux function. By reversing the order of the scaling filter vector and
multiplying every even element (indexing from 1) by (-1), you obtain the high-pass
filter.
Repeatedly upsampling by two and convolving the output with the scaling filter produces the Daubechies' extremal phase wavelet.
L = dbaux(2); H = wrev(L).*[1 -1 1 -1]; HU = dyadup(H,0); HU = conv(HU,L); plot(HU); title('1st Iteration'); H1 = conv(dyadup(HU,0),L); H2 = conv(dyadup(H1,0),L); H3 = conv(dyadup(H2,0),L); H4 = conv(dyadup(H3,0),L); figure; for k =1:4 subplot(2,2,k); eval(['plot(H' num2str(k) ')']); axis tight; end
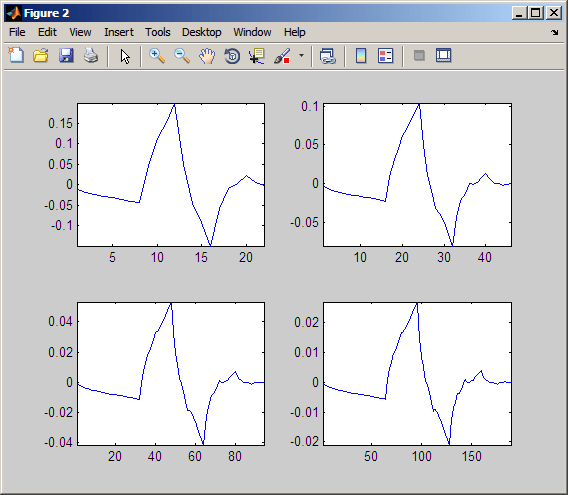
The curve begins to look progressively more like the db2 wavelet.
This means that the wavelet's shape is determined entirely by the coefficients of the
reconstruction filters.
This relationship has profound implications. It means that you cannot choose just any shape, call it a wavelet, and perform an analysis. At least, you can't choose an arbitrary wavelet waveform if you want to be able to reconstruct the original signal accurately. You are compelled to choose a shape determined by quadrature mirror decomposition filters.
Scaling Function
We've seen the interrelation of wavelets and quadrature mirror filters. The wavelet function ψ is determined by the high-pass filter, which also produces the details of the wavelet decomposition.
There is an additional function associated with some, but not all, wavelets. This is the so-called scaling function, ϕ. The scaling function is very similar to the wavelet function. It is determined by the low-pass quadrature mirror filters, and thus is associated with the approximations of the wavelet decomposition.
In the same way that iteratively upsampling and convolving the high-pass filter produces a shape approximating the wavelet function, iteratively upsampling and convolving the low-pass filter produces a shape approximating the scaling function.
