cwt
Continuous 1-D wavelet transform
Syntax
Description
wt = cwt(x)x.
The
CWT is obtained using the analytic Morse wavelet with the symmetry parameter,
gamma (), equal to 3 and the time-bandwidth product equal to 60.
cwt uses 10 voices per octave. The minimum and maximum
scales are determined automatically based on the energy spread of the wavelet in
frequency and time.
The cwt function uses L1 normalization. With L1
normalization, if you have equal amplitude oscillatory components in your data
at different scales, they will have equal magnitude in the CWT. Using L1
normalization shows a more accurate representation of the signal. See L1 Norm for CWT and Continuous Wavelet Transform of Two Complex Exponentials.
[___,
returns the filter bank used in the CWT. See coi,fb] = cwt(___)cwtfilterbank.
[___,
returns the scaling coefficients for the wavelet transform.fb,scalingcfs] = cwt(___)
[___] = cwt(___,
specifies one or more additional name-value arguments. For example, Name=Value)wt
= cwt(x,TimeBandwidth=40,VoicesPerOctave=20) specifies a
time-bandwidth product of 40 and 20 voices per octave.
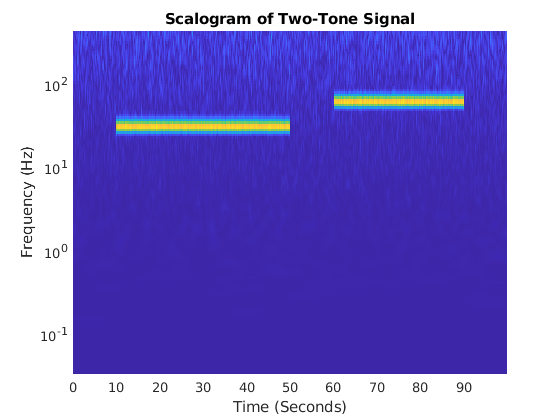
cwt(___) with no output arguments plots the
CWT scalogram. The scalogram is the absolute value of the CWT plotted as a
function of time and frequency. Frequency is plotted on a logarithmic scale. The
cone of influence showing where edge effects become significant is also plotted.
Gray regions outside the dashed white line delineate regions where edge effects
are significant. If the input signal is complex-valued, the positive
(counterclockwise) and negative (clockwise) components are plotted in separate
scalograms.
If you do not specify a sampling frequency or sampling period, the frequencies are plotted in cycles per sample. If you specify a sampling frequency, the frequencies are in hertz. If you specify a sampling period, the scalogram is plotted as a function of time and periods. If the input signal is a timetable, the scalogram is plotted as a function of time and frequency in hertz and uses the RowTimes as the basis for the time axis.
To see the time, frequency, and magnitude of a scalogram point, enable data tips in the figure axes toolbar and click the desired point in the scalogram.

Note
Before plotting, cwt clears (clf) the current
figure. To plot the scalogram in a subplot, use a plotting function. See
Plot CWT Scalogram in Subplot.
Examples
Input Arguments
Output Arguments
More About
Tips
The syntax for the old
cwtfunction continues to work but is no longer recommended. Use the current version ofcwt. Both the old and current versions use the same function name. The inputs to the function determine automatically which version is used. See cwt function syntax has changed.When performing multiple CWTs, for example inside a for-loop, the recommended workflow is to first create a
cwtfilterbankobject and then use thewtobject function. This workflow minimizes overhead and maximizes performance. See Using CWT Filter Bank on Multiple Time Series.
Algorithms
References
[1] Lilly, J. M., and S. C. Olhede. “Generalized Morse Wavelets as a Superfamily of Analytic Wavelets.” IEEE Transactions on Signal Processing 60, no. 11 (November 2012): 6036–6041. https://doi.org/10.1109/TSP.2012.2210890.
[2] Lilly, J.M., and S.C. Olhede. “Higher-Order Properties of Analytic Wavelets.” IEEE Transactions on Signal Processing 57, no. 1 (January 2009): 146–160. https://doi.org/10.1109/TSP.2008.2007607.
[3] Lilly, J. M. jLab: A data analysis package for MATLAB®, version 1.6.2. 2016. http://www.jmlilly.net/jmlsoft.html.
[4] Lilly, Jonathan M. “Element Analysis: A Wavelet-Based Method for Analysing Time-Localized Events in Noisy Time Series.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 473, no. 2200 (April 30, 2017): 20160776. https://doi.org/10.1098/rspa.2016.0776.