dddtree
Dual-tree and double-density 1-D wavelet transform
Syntax
Description
wt = dddtree(typetree,x,level,fdf,df)typetree discrete wavelet transform (DWT) of the 1-D input
signal, x, down to level, level. The wavelet transform
uses the decomposition (analysis) filters, fdf, for the first level and the
analysis filters, df, for subsequent levels. Supported wavelet transforms
are the critically sampled DWT, double-density, dual-tree complex, and dual-tree double-density
complex wavelet transform. The critically sampled DWT is a filter bank decomposition in an
orthogonal or biorthogonal basis (nonredundant). The other wavelet transforms are oversampled
filter banks.
wt = dddtree(typetree,x,level,fname1,fname2)fname1 for the first
stage of the dual-tree wavelet transform and the filters specified
in fname2 for subsequent stages of the dual-tree
wavelet transform. Specifying different filters for stage 1 is valid
and necessary only when typetree is 'cplxdt' or 'cplxdddt'.
Examples
Complex Dual-Tree Wavelet Transform
Obtain the complex dual-tree wavelet transform of the noisy Doppler signal. The FIR filters in the first and subsequent stages result in an approximately analytic wavelet as required.
Use dtfilters to create the first-stage Farras analysis filters and 6-tap Kingsbury Q-shift analysis filters for the subsequent stages of the multiresolution analysis.
df = dtfilters('dtf1');The Farras and Kingsbury filters are in df{1} and df{2}, respectively. Load the noisy Doppler signal and obtain the complex dual-tree wavelet transform down to level 4.
load noisdopp; wt = dddtree('cplxdt',noisdopp,4,df{1},df{2});
Plot an approximation based on the level-four approximation coefficients.
xapp = dddtreecfs('r',wt,'scale',{5}); plot(noisdopp) hold on plot(cell2mat(xapp),'r','linewidth',3) axis tight
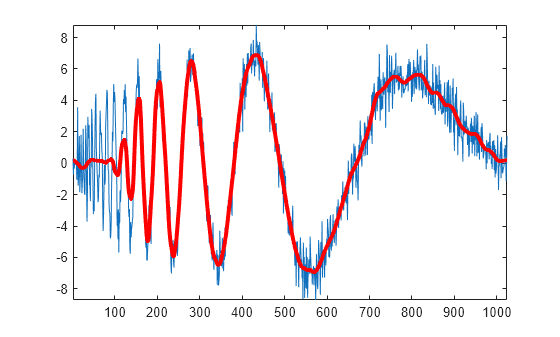
Using the output of dtfilters, or the filter name itself, in dddtree is preferable to manually entering truncated filter coefficients. To demonstrate the negative impact on signal reconstruction, create truncated versions of the Farras and Kingsbury analysis filters. Display the differences between the truncated and original filters.
Faf{1} = [0 0
-0.0884 -0.0112
0.0884 0.0112
0.6959 0.0884
0.6959 0.0884
0.0884 -0.6959
-0.0884 0.6959
0.0112 -0.0884
0.0112 -0.0884
0 0];
Faf{2} = [ 0.0112 0
0.0112 0
-0.0884 -0.0884
0.0884 -0.0884
0.6959 0.6959
0.6959 -0.6959
0.0884 0.0884
-0.0884 0.0884
0 0.0112
0 -0.0112];
af{1} = [ 0.0352 0
0 0
-0.0883 -0.1143
0.2339 0
0.7603 0.5875
0.5875 -0.7603
0 0.2339
-0.1143 0.0883
0 0
0 -0.0352];
af{2} = [0 -0.0352
0 0
-0.1143 0.0883
0 0.2339
0.5875 -0.7603
0.7603 0.5875
0.2339 0
-0.0883 -0.1143
0 0
0.0352 0];
max(max(abs(df{1}{1}-Faf{1})))ans = 2.6792e-05
max(max(abs(df{1}{2}-Faf{2})))ans = 2.6792e-05
max(max(abs(df{2}{1}-af{1})))ans = 3.6160e-05
max(max(abs(df{2}{2}-af{2})))ans = 3.6160e-05
Obtain the complex dual-tree wavelet transform down to level 4 using the truncated filters. Take the inverse transform and compare the reconstruction with the original signal.
wt = dddtree('cplxdt',noisdopp,4,Faf,af);
xrec = idddtree(wt);
max(abs(noisdopp-xrec))ans = 0.0024
Do the same using the filter name. Confirm the difference is smaller.
wt = dddtree('cplxdt',noisdopp,4,'dtf1'); xrec = idddtree(wt); max(abs(noisdopp-xrec))
ans = 2.1893e-07
Double-Density Wavelet Transform
Obtain the double-density wavelet transform of a signal with two discontinuities. Use the level-one detail coefficients to localize the discontinuities.
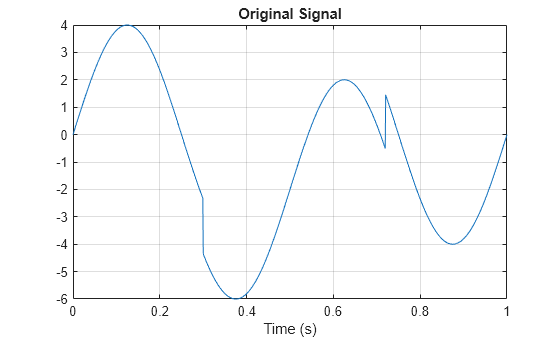
Create a signal consisting of a 2-Hz sine wave with a duration of 1 second. The sine wave has discontinuities at 0.3 and 0.72 seconds.
N = 1024; t = linspace(0,1,1024); x = 4*sin(4*pi*t); x = x - sign(t - .3) - sign(.72 - t); plot(t,x) xlabel('Time (s)') title('Original Signal') grid on
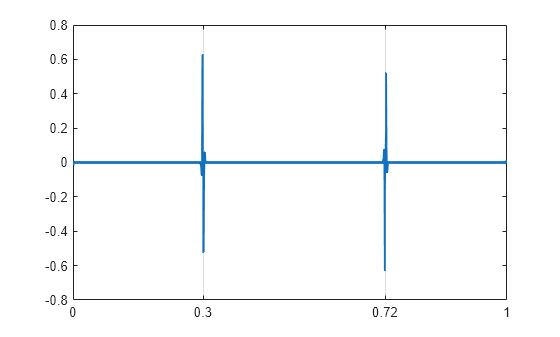
Obtain the double-density wavelet transform of the signal. Reconstruct an approximation based on the level-one detail coefficients by first setting the lowpass (scaling) coefficients equal to 0. Plot the result. Observe features in the reconstruction align with the signal discontinuities.
wt = dddtree('ddt',x,1,'filters1'); wt.cfs{2} = zeros(1,512); xrec = idddtree(wt); plot(t,xrec,'linewidth',2) set(gca,'xtick',[0 0.3 0.72 1]) set(gca,'xgrid','on')
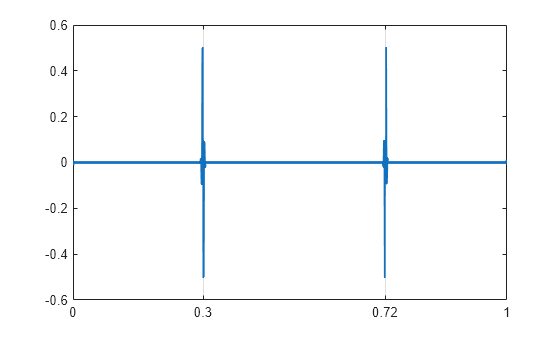
First-Level Detail Coefficients Approximation — Complex Dual-Tree
Obtain the complex dual-tree wavelet transform of a signal with two discontinuities. Use the first-level detail coefficients to localize the discontinuities.
Create a signal consisting of a 2-Hz sine wave with a duration of 1 second. The sine wave has discontinuities at 0.3 and 0.72 seconds.
N = 1024; t = linspace(0,1,1024); x = 4*sin(4*pi*t); x = x - sign(t - .3) - sign(.72 - t); plot(t,x) xlabel('Time (s)') title('Original Signal') grid on

Obtain the dual-tree wavelet transform of the signal, reconstruct an approximation based on the level-one detail coefficients, and plot the result.
wt = dddtree('cplxdt',x,1,'FSfarras','qshift06'); wt.cfs{2} = zeros(1,512,2); xrec = idddtree(wt); plot(t,xrec,'linewidth',2) set(gca,'xtick',[0 0.3 0.72 1]) set(gca,'xgrid','on')
Input Arguments
typetree — Type of wavelet decomposition
'dwt' | 'ddt' | 'cplxdt' | 'cplxdddt'
Type of wavelet decomposition, specified as one of 'dwt', 'ddt', 'cplxdt',
or 'cplxdddt'. The type, 'dwt',
gives a critically sampled (nonredundant) discrete wavelet transform.
The other decomposition types produce oversampled wavelet transforms. 'ddt' produces
a double-density wavelet transform. 'cplxdt' produces
a dual-tree complex wavelet transform. 'cplxdddt' produces
a double-density dual-tree complex wavelet transform.
x — Input signal
vector
Input signal, specified as an even-length row or column vector. If L is the
value of the level of the wavelet decomposition,
2L must divide the length of
x. Additionally, the length of the signal must be greater than or equal
to the product of the maximum length of the decomposition (analysis) filters and
2(L-1).
Data Types: double
level — Level of wavelet decomposition
positive integer
Level of the wavelet decomposition, specified as an integer. If L is the
value of level, 2L must
divide the length of x. Additionally, the length of the signal must be
greater than or equal to the product of the maximum length of the decomposition (analysis)
filters and 2(L-1).
Data Types: double
fdf — Level-one analysis filters
matrix | cell array
The level-one analysis filters, specified as a matrix or cell
array of matrices. Specify fdf as a matrix when typetree is 'dwt' or 'ddt'.
The size and structure of the matrix depend on the typetree input
as follows:
'dwt'— This is the critically sampled discrete wavelet transform. In this case,fdfis a two-column matrix with the lowpass (scaling) filter in the first column and the highpass (wavelet) filter in the second column.'ddt'— This is the double-density wavelet transform. The double-density DWT is a three-channel perfect reconstruction filter bank.fdfis a three-column matrix with the lowpass (scaling) filter in the first column and the two highpass (wavelet) filters in the second and third columns. In the double-density wavelet transform, the single lowpass and two highpass filters constitute a three-channel perfect reconstruction filter bank. This is equivalent to the three filters forming a tight frame. You cannot arbitrarily choose the two wavelet filters in the double-density DWT. The three filters together must form a tight frame.
Specify fdf as a 1-by-2 cell array of matrices
when typetree is a dual-tree transform, 'cplxdt' or 'cplxdddt'.
The size and structure of the matrix elements depend on the typetree input
as follows:
For the dual-tree complex wavelet transform,
'cplxdt',fdf{1}is a two-column matrix containing the lowpass (scaling) filter and highpass (wavelet) filters for the first tree. The scaling filter is the first column and the wavelet filter is the second column.fdf{2}is a two-column matrix containing the lowpass (scaling) and highpass (wavelet) filters for the second tree. The scaling filter is the first column and the wavelet filter is the second column.For the double-density dual-tree complex wavelet transform,
'cplxdddt',fdf{1}is a three-column matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the first tree andfdf{2}is a three-column matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the second tree.
Data Types: double
df — Analysis filters for levels > 1
matrix | cell array
Analysis filters for levels > 1, specified as a matrix or
cell array of matrices. Specify df as a matrix
when typetree is 'dwt' or 'ddt'.
The size and structure of the matrix depend on the typetree input
as follows:
'dwt'— This is the critically sampled discrete wavelet transform. In this case,dfis a two-column matrix with the lowpass (scaling) filter in the first column and the highpass (wavelet) filter in the second column. For the critically sampled orthogonal or biorthogonal DWT, the filters indfandfdfmust be identical.'ddt'— This is the double-density wavelet transform. The double-density DWT is a three-channel perfect reconstruction filter bank.dfis a three-column matrix with the lowpass (scaling) filter in the first column and the two highpass (wavelet) filters in the second and third columns. In the double-density wavelet transform, the single lowpass and two highpass filters must constitute a three-channel perfect reconstruction filter bank. This is equivalent to the three filters forming a tight frame. For the double-density DWT, the filters indfandfdfmust be identical.
Specify df as a 1-by-2 cell array of matrices
when typetree is a dual-tree transform, 'cplxdt' or 'cplxdddt'.
For dual-tree transforms, the filters in fdf and df must
be different. The size and structure of the matrix elements in the
cell array depend on the typetree input as follows:
For the dual-tree complex wavelet transform,
'cplxdt',df{1}is a two-column matrix containing the lowpass (scaling) and highpass (wavelet) filters for the first tree. The scaling filter is the first column and the wavelet filter is the second column.df{2}is a two-column matrix containing the lowpass (scaling) and highpass (wavelet) filters for the second tree. The scaling filter is the first column and the wavelet filter is the second column.For the double-density dual-tree complex wavelet transform,
'cplxdddt',df{1}is a three-column matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the first tree anddf{2}is a three-column matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the second tree.
Data Types: double
fname — Filter name
character vector | string scalar
Filter name, specified as a character vector or string scalar. For the critically sampled DWT,
specify any valid orthogonal or biorthogonal wavelet filter. See wfilters for details. For the double-density wavelet transform,
'ddt', valid choices are 'filters1',
'filters2', and 'doubledualfilt'. For the complex
dual-tree wavelet transform, valid choices are 'dtfP' with P = 1, 2, 3, 4.
For the double-density dual-tree wavelet transform, the only valid choice is
'dddtf1'. See dtfilters for more details on valid filter
names for the oversampled wavelet filter banks.
Data Types: char
fname1 — First-stage filter name
character vector | string scalar
First-stage filter name, specified as a character vector or string scalar. Specifying a
different filter for the first stage is valid and necessary only in the dual-tree transforms,
'cplxdt' and 'cplxdddt'. In the complex dual-tree
wavelet transform, you can use any valid wavelet filter for the first stage. In the
double-density dual-tree wavelet transform, the first-stage filters must form a three-channel
perfect reconstruction filter bank.
Data Types: char
fname2 — Filter name for stages > 1
character vector | string scalar
Filter name for stages > 1, specified as a character vector or string scalar. You must
specify a first-level filter that is different from the wavelet and scaling filters in
subsequent levels when using the dual-tree wavelet transforms, 'cplxdt' or
'cplxdddt'. See dtfilters for valid choices.
Data Types: char
Output Arguments
wt — Wavelet transform
structure
Wavelet transform, returned as a structure with these fields:
type — Type of wavelet decomposition (filter bank)
'dwt' | 'ddt' | 'cplxdt' | 'cplxdddt'
Type of wavelet decomposition (filter bank) used in the analysis,
returned as one of 'dwt', 'ddt', 'cplxdt',
or 'cplxdddt'. The type, 'dwt',
gives a critically sampled discrete wavelet transform. The other types
correspond to oversampled wavelet transforms. 'ddt' is
a double-density wavelet transform, 'cplxdt' is
a dual-tree complex wavelet transform, and 'cplxdddt' is
a double-density dual-tree complex wavelet transform.
level — Level of the wavelet decomposition
positive integer
Level of wavelet decomposition, returned as a positive integer.
filters — Decomposition (analysis) and reconstruction (synthesis) filters
structure
Decomposition (analysis) and reconstruction (synthesis) filters, returned as a structure with these fields:
FDf — First-stage analysis filters
matrix | cell array
First-stage analysis filters, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the first-stage analysis filters for the corresponding tree.
Df — Analysis filters for levels > 1
matrix | cell array
Analysis filters for levels > 1, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the analysis filters for the corresponding tree.
FRf — First-level reconstruction filters
matrix | cell array
First-level reconstruction filters, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the first-stage synthesis filters for the corresponding tree.
Rf — Reconstruction filters for levels > 1
matrix | cell array
Reconstruction filters for levels > 1, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the synthesis filters for the corresponding tree.
cfs — Wavelet transform coefficients
cell array of matrices
Wavelet transform coefficients, returned as a 1-by-(level+1)
cell array of matrices. The size and structure of the matrix elements
of the cell array depend on the type of wavelet transform, typetree,
as follows:
'dwt'—cfs{j}j = 1,2,...
levelis the level.cfs{level+1}are the lowpass, or scaling, coefficients.
'ddt'—cfs{j}(:,:,k)j = 1,2,...
levelis the level.k = 1,2 is the wavelet filter.
cfs{level+1}(:,:)are the lowpass, or scaling, coefficients.
'cplxdt'—cfs{j}(:,:,m)j = 1,2,...
levelis the level.m = 1,2 are the real and imaginary parts.
cfs{level+1}(:,:,m)are the lowpass, or scaling, coefficients.
'cplxdddt'—cfs{j}(:,:,k,m)j = 1,2,...
levelis the level.k = 1,2 is the wavelet filter.
m = 1,2 are the real and imaginary parts.
cfs{level+1}(:,:,m)are the lowpass, or scaling, coefficients.
Version History
Introduced in R2013b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)