wavedec
Multilevel 1-D discrete wavelet transform
Description
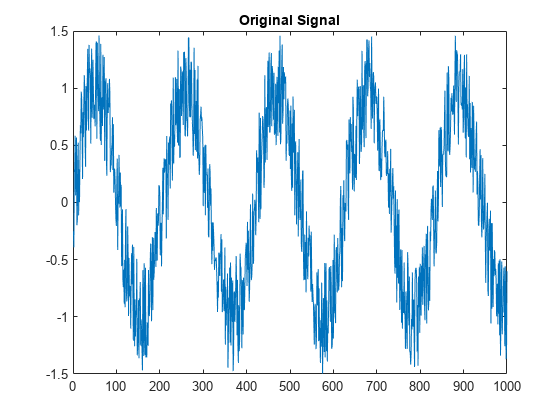
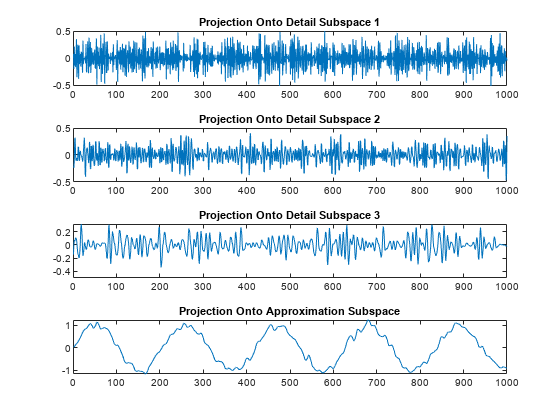
Examples
Input Arguments
Output Arguments
Algorithms
Given a signal s of length N, the DWT consists
of at most log2
N steps. Starting from s, the first step produces
two sets of coefficients: approximation coefficients
cA1 and detail coefficients
cD1. Convolving s
with the lowpass filter LoD and the highpass filter
HiD, followed by dyadic decimation (downsampling by 2), results
in the approximation and detail coefficients respectively.
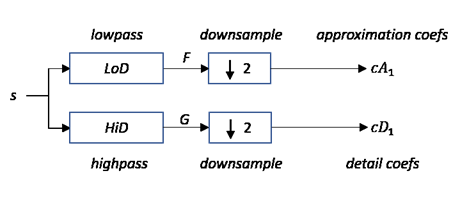
where
 — Convolve with filter X
— Convolve with filter X— Downsample (keep the even-indexed elements)
The length of each filter is equal to 2n. If N = length(s), the signals F and G are of length N + 2n −1 and the coefficients cA1 and cD1 are of length
floor.
The next step splits the approximation coefficients cA1 in two parts using the same scheme, replacing s by cA1, and producing cA2 and cD2, and so on.

The wavelet decomposition of the signal s analyzed at level j has the following structure: [cAj, cDj, ..., cD1].
This structure contains, for j = 3, the terminal nodes of the following tree:

References
[1] Daubechies, I. Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: SIAM Ed, 1992.
[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.