wbmpen
Penalized threshold for wavelet 1-D or 2-D denoising
Description
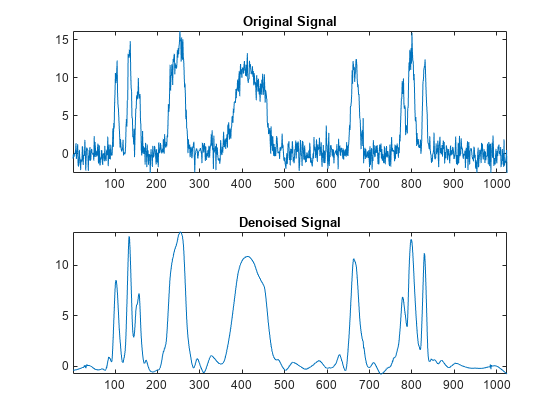
thr = wbmpen(c,l,sigma,alpha)thr for denoising.
c,l is the wavelet decomposition structure of the signal or
image to be denoised. sigma is the standard deviation of the
zero mean Gaussian white noise in the denoising model (see wnoisest for more information).
alpha is a tuning parameter for the penalty term.
thr = wbmpen(c,l,sigma,alpha,ARG)
2×sigma^2×t×(alpha + log(n/t))sum(c(k)^2,k≤t)crit(t)
where n is the number of coefficients and
crit(t) = -sum(c(k)^2,k≤t) + 2×sigma^2×t×(alpha + log(n/t)).
Examples
Input Arguments
Output Arguments
More About
References
[1] Birgé, Lucien, and Pascal Massart. “From Model Selection to Adaptive Estimation.” In Festschrift for Lucien Le Cam, edited by David Pollard, Erik Torgersen, and Grace L. Yang, 55–87. New York, NY: Springer New York, 1997. https://doi.org/10.1007/978-1-4612-1880-7_4.
Version History
Introduced before R2006a