wrcoef
Reconstruct single branch from 1-D wavelet coefficients
Description
x = wrcoef(type,c,l,wname)type based on the
wavelet decomposition structure [c,l] of a 1-D signal (see
wavedec for more information)
using the wavelet specified by wname. The coefficients at the
maximum decomposition level are reconstructed. The length of x
is equal to the length of the original 1-D signal.
Examples
Reconstruct Wavelet Coefficients
Load a 1-D signal.
load sumsin
s = sumsin;Perform a level 5 wavelet decomposition of the signal using the sym4 wavelet.
[c,l] = wavedec(s,5,'sym4');Reconstruct the approximation coefficients at level 5 from the wavelet decomposition structure [c,l].
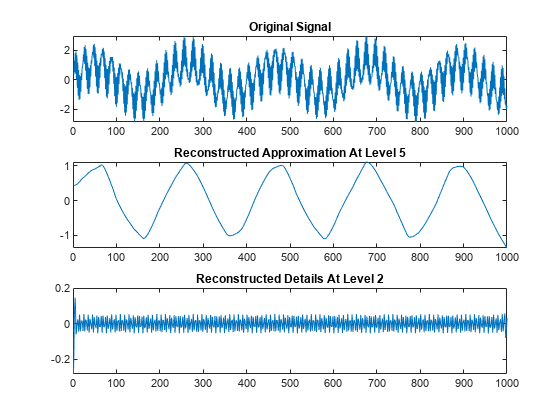
a5 = wrcoef('a',c,l,'sym4');
Reconstruct the detail coefficients at level 2.
d2 = wrcoef('d',c,l,'sym4',2);
Plot the original signal and reconstructed coefficients.
subplot(3,1,1) plot(s) title('Original Signal') subplot(3,1,2) plot(a5) title('Reconstructed Approximation At Level 5') subplot(3,1,3) plot(d2) title('Reconstructed Details At Level 2')
Multiresolution Analysis Based on Decimated Discrete Wavelet Transform
This example shows how, starting with a multilevel 1-D discrete wavelet decomposition of a signal, you can obtain projections of the signal onto wavelet subspaces at successive scales and a scaling subspace. These projections are at the same time scale as the original signal. In other words, you can obtain a multiresolution analysis (MRA) based on the decimated discrete wavelet transform (DWT). You can recover the signal by summing the projections. For more information, see Practical Introduction to Multiresolution Analysis.
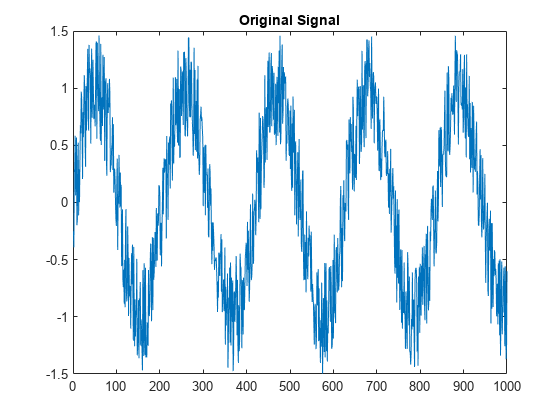
Load and plot a signal.
load noissin plot(noissin) title("Original Signal")
Use the wavedec function to obtain the discrete wavelet decomposition of the signal down to level 3 using the db4 wavelet.
level = 3;
wv = "db4";
[C,L] = wavedec(noissin,level,wv);Preallocate a matrix to save the MRA. The number of rows is one more than the level of decomposition, and the number of columns equals the length of the signal.
mra = zeros(level+1,numel(noissin));
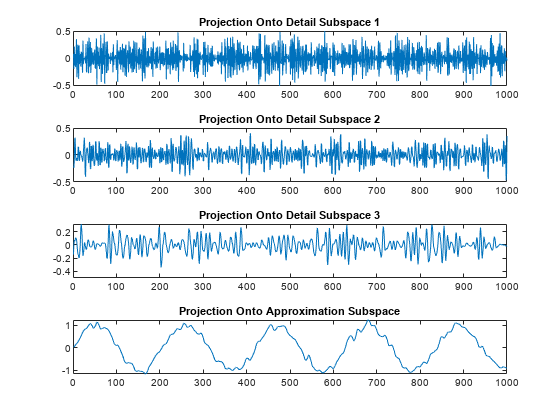
Use the wrcoef function to obtain the projections of the signal onto the three wavelet (detail) subspaces. Then obtain the projection onto the final scaling (coarse or approximation) subspace.
for k=1:level mra(k,:) = wrcoef("d",C,L,wv,k); end mra(end,:) = wrcoef("a",C,L,wv,level);
Confirm the sum along the rows of the MRA equals the original signal.
mraSum = sum(mra,1); max(abs(mraSum-noissin))
ans = 1.6591e-12
Plot the MRA.
tiledlayout(level+1,1) for k=1:level nexttile plot(mra(k,:)) title("Projection Onto Detail Subspace "+num2str(k)) end nexttile plot(mra(end,:)) title("Projection Onto Approximation Subspace")
Input Arguments
type — Coefficients to reconstruct
'a' | 'd'
Coefficients to reconstruct, specified as 'a' or
'd', for approximation or detail coefficients,
respectively.
wname — Analyzing wavelet
character vector | string scalar
Analyzing wavelet used to create the wavelet decomposition structure
[c,l], specified as a character vector or string
scalar. wrcoef supports only orthogonal or biorthogonal
wavelets. See wfilters.
LoR,HiR — Wavelet reconstruction filters
even-length real-valued vectors
Wavelet reconstruction filters, specified as a pair of even-length
real-valued vectors. LoR is the lowpass reconstruction
filter, and HiR is the highpass reconstruction filter.
The lengths of LoR and HiR must be
equal. See wfilters for additional
information.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)