Matching Pursuit Algorithms
Redundant Dictionaries and Sparsity
Representing a signal in a particular basis involves finding the unique set of expansion coefficients in that basis. While there are many advantages to signal representation in a basis, particularly an orthogonal basis, there are also disadvantages.
The ability of a basis to provide a sparse representation depends on how well the signal characteristics match the characteristics of the basis vectors. For example, smooth continuous signals are sparsely represented in a Fourier basis, while impulses are not. A smooth signal with isolated discontinuities is sparsely represented in a wavelet basis. However, a wavelet basis is not efficient at representing a signal whose Fourier transform has narrow high frequency support.
Real-world signals often contain features that prohibit sparse representation in any single basis. For these signals, you want the ability to choose vectors from a set not limited to a single basis. Because you want to ensure that you can represent every vector in the space, the dictionary of vectors you choose from must span the space. However, because the set is not limited to a single basis, the dictionary is not linearly independent.
Because the vectors in the dictionary are not a linearly independent set, the signal representation in the dictionary is not unique. However, by creating a redundant dictionary, you can expand your signal in a set of vectors that adapt to the time-frequency or time-scale characteristics of your signal. You are free to create a dictionary consisting of the union of several bases. For example, you can form a basis for the space of square-integrable functions consisting of a wavelet packet basis and a local cosine basis. A wavelet packet basis is well adapted to signals with different behavior in different frequency intervals. A local cosine basis is well adapted to signals with different behavior in different time intervals. The ability to choose vectors from each of these bases greatly increases your ability to sparsely represent signals with varying characteristics.
Nonlinear Approximation in Dictionaries
Define a dictionary as a collection of unit-norm elementary building blocks for your signal space. These unit-norm vectors are called atoms. If the atoms of the dictionary span the entire signal space, the dictionary is complete.
If the dictionary atoms form a linearly-dependent set, the dictionary is redundant. In most applications of matching pursuit, the dictionary is complete and redundant.
Let {φk} denote the atoms of a dictionary. Assume the dictionary is complete and redundant. There is no unique way to represent a signal from the space as a linear combination of the atoms.
An important question is whether there exists a best way. An intuitively satisfying way to choose the best representation is to select the φk yielding the largest inner products (in absolute value) with the signal. For example, the best single φk is
which for a unit-norm atom is the magnitude of the scalar projection onto the subspace spanned by φk.
The central problem in matching pursuit is how you choose the optimal M-term expansion of your signal in a dictionary.
Basic Matching Pursuit
Let Φ denote the dictionary of atoms as a N-by-M matrix with M>N. If the complete, redundant dictionary forms a frame for the signal space, you can obtain the minimum L2 norm expansion coefficient vector by using the frame operator.
However, the coefficient vector returned by the frame operator does not preserve sparsity. If the signal is sparse in the dictionary, the expansion coefficients obtained with the canonical frame operator generally do not reflect that sparsity. Sparsity of your signal in the dictionary is a trait that you typically want to preserve. Matching pursuit addresses sparsity preservation directly.
Matching pursuit is a greedy algorithm that computes the best nonlinear approximation to a signal in a complete, redundant dictionary. Matching pursuit builds a sequence of sparse approximations to the signal stepwise. Let Φ= {φk} denote a dictionary of unit-norm atoms. Let f be your signal.
Start by defining R0f = f
Begin the matching pursuit by selecting the atom from the dictionary that maximizes the absolute value of the inner product with R0f = f. Denote that atom by φp.
Form the residual R1f by subtracting the orthogonal projection of R0f onto the space spanned by φp.
Iterate by repeating steps 2 and 3 on the residual.
Stop the algorithm when you reach some specified stopping criterion.
In nonorthogonal (or basic) matching pursuit, the dictionary atoms are not mutually orthogonal vectors. Therefore, subtracting subsequent residuals from the previous one can introduce components that are not orthogonal to the span of previously included atoms.
To illustrate this, consider the following example. The example is not intended to present a working matching pursuit algorithm.
Consider the following dictionary for Euclidean 2-space. This dictionary is an equal-norm frame.
Assume you have the following signal.
The following figure illustrates this example. The dictionary atoms are in red. The signal vector is in blue.
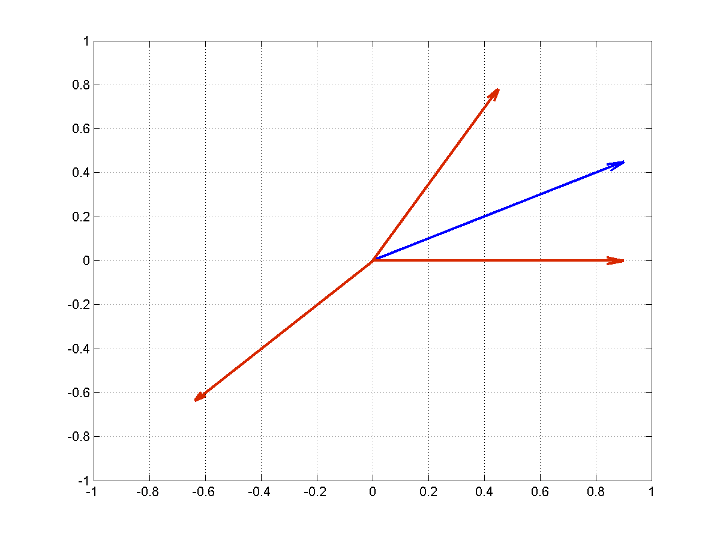
Construct this dictionary and signal in MATLAB®.
dictionary = [1 0; 1/2 sqrt(3)/2; -1/sqrt(2) -1/sqrt(2)]'; x = [1 1/2]';
Compute the inner (scalar) products between the signal and the dictionary atoms.
scalarproducts = dictionary'*x;
The largest scalar product in absolute value occurs between
the signal and [-1/sqrt(2); -1/sqrt(2)]. This is
clear because the angle between the two vectors is almost π
radians.
Form the residual by subtracting the orthogonal projection of
the signal onto [-1/sqrt(2); -1/sqrt(2)] from the
signal. Next, compute the inner products of the residual (new signal)
with the remaining dictionary atoms. It is not necessary to include [-1/sqrt(2);
-1/sqrt(2)] because the residual is orthogonal to that vector
by construction.
residual = x-scalarproducts(3)*dictionary(:,3); scalarproducts = dictionary(:,1:2)'*residual;
The largest scalar product in absolute value is obtained with [1;0].
The best two atoms in the dictionary from two iterations are [-1/sqrt(2);
-1/sqrt(2)] and [1;0]. If you iterate
on the residual, you see that the output is no longer orthogonal to
the first atom chosen. In other words, the algorithm has introduced
a component that is not orthogonal to the span of the first atom selected.
This fact and the associated complications with convergence argues
in favor of Orthogonal Matching Pursuit (OMP).
Orthogonal Matching Pursuit
In orthogonal matching pursuit (OMP), the residual is always orthogonal to the span of the atoms already selected. This results in convergence for a d-dimensional vector after at most d steps.
Conceptually, you can do this by using Gram-Schmidt to create an orthonormal set of atoms. With an orthonormal set of atoms, you see that for a d-dimensional vector, you can find at most d orthogonal directions.
The OMP algorithm is:
Denote your signal by f. Initialize the residual R0f = f.
Select the atom that maximizes the absolute value of the inner product with R0f = f. Denote that atom by φp.
Form a matrix, Φ, with previously selected atoms as the columns. Define the orthogonal projection operator onto the span of the columns of Φ.
Apply the orthogonal projection operator to the residual.
Update the residual.
I is the identity matrix.
Orthogonal matching pursuit ensures that components in the span of previously selected atoms are not introduced in subsequent steps.
Weak Orthogonal Matching Pursuit
It can be computationally efficient to relax the criterion that the selected atom maximizes the absolute value of the inner product to a less strict one.
This is known as weak matching pursuit.
