Delay Profile and Fluorescent Lighting Effects
This example demonstrates the impact of changing the TGac delay profile, and it shows how fluorescent lighting affects the time response of the channel.
Delay Profile Effects
Create VHT configuration object. Set the sample rate to 80 MHz.
cfgVHT = wlanVHTConfig; fs = 80e6;
Generate random binary data and create a transmit waveform parameterized by the VHT configuration object.
d = randi([0 1],8*cfgVHT.PSDULength,1); testWaveform = wlanWaveformGenerator(d,cfgVHT);
Create a TGac channel object. Set the delay profile to 'Model-A', which corresponds to flat fading. Disable large-scale fading effects.
tgacChan = wlanTGacChannel('SampleRate',fs, ... 'ChannelBandwidth',cfgVHT.ChannelBandwidth, ... 'DelayProfile','Model-A', ... 'LargeScaleFadingEffect','None');
Pass the transmitted waveform through the TGac channel.
rxModelA = tgacChan(testWaveform);
Set the delay profile to Model-C, which corresponds to a multipath channel with 14 distinct paths and a 30 ns RMS delay spread. The maximum delay spread is 200 ns, which corresponds to a coherence bandwidth of 2.5 MHz.
release(tgacChan)
tgacChan.DelayProfile = 'Model-C';Pass the waveform through the model-C channel.
rxModelC = tgacChan(testWaveform);
Create a spectrum analyzer and use it to visualize the spectrum of the received signals.
saScope = spectrumAnalyzer(SampleRate=fs, ... ShowLegend=true,ChannelNames={'Model-A','Model-C'},... AveragingMethod='exponential',ForgettingFactor=0.99); saScope([rxModelA rxModelC])
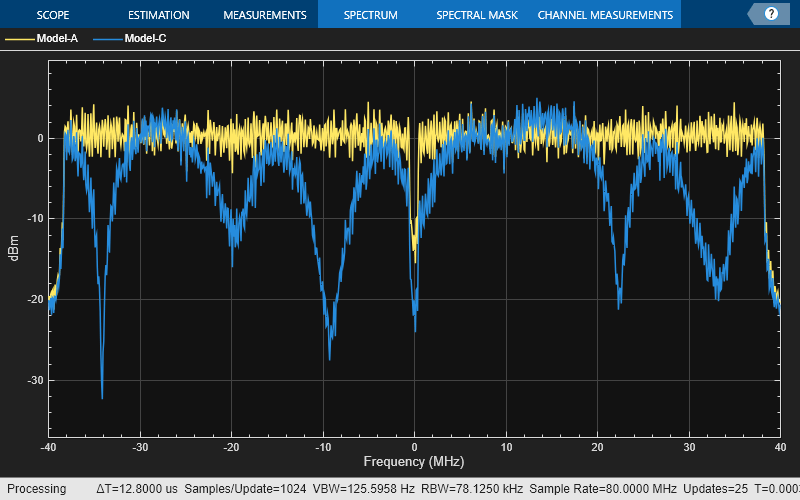
As expected, the frequency response of the model-A signal is flat across the 80 MHz bandwidth. Conversely, the model-C frequency response varies because its coherence bandwidth is much smaller than the channel bandwidth.
Fluorescent Effects
Release the TGac channel, and set its delay profile to 'Model-D'. Disable the fluorescent lighting effect.
release(tgacChan)
tgacChan.DelayProfile = 'Model-D';
tgacChan.FluorescentEffect = false;To better illustrate the Doppler effects of fluorescent lighting, change the bandwidth and sample rate of the channel. Generate a test waveform of ones.
tgacChan.ChannelBandwidth = 'CBW20';
fs = 20e6;
tgacChan.SampleRate = fs;
testWaveform = ones(5e5,1);To ensure repeatability, set the global random number generator to a fixed value.
rng(37)
Pass the waveform through the TGac channel.
rxSig0 = tgacChan(testWaveform);
Enable the fluorescent lighting effect. Reset the random number generator, and pass the waveform through the channel.
release(tgacChan) tgacChan.FluorescentEffect = true; rng(37) rxSig1 = tgacChan(testWaveform);
Determine the time axis and channel filter delay.
t = ((1:size(rxSig0,1))'-1)/fs; fDelay = tgacChan.info.ChannelFilterDelay;
Plot the magnitude of the received signals while accounting for the channel filter delay.
plot(t(fDelay+1:end),[abs(rxSig0(fDelay+1:end)) abs(rxSig1(fDelay+1:end))]) xlabel('Time (s)') ylabel('Magnitude (V)') legend('Fluorescent Off','Fluorescent On','location','best')
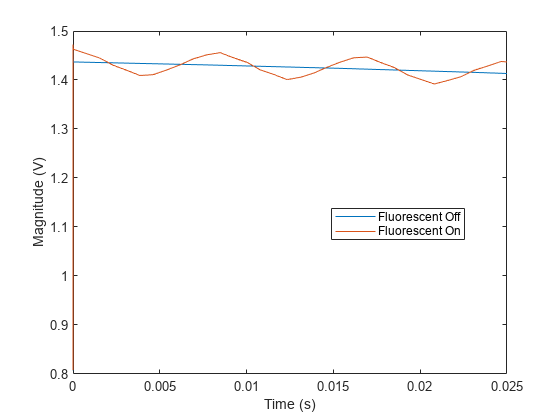
Fluorescent lighting introduces a Doppler component at twice the power line frequency (120 Hz in the U.S.).
Confirm that the peaks are separated by approximately 0.0083 s (inverse of 120 Hz) by measuring distance between the second and third peaks.
[~,loc] = findpeaks(abs(rxSig1(1e5:4e5))); peakTimes = loc/fs; peakSeparation = diff(peakTimes)
peakSeparation = 0.0085
