bufferm2
bufferm2.m Documentation
This function is mostly a legacy one. In early versions of the Mapping Toolbox (circa 2005 or so), the bufferm.m function included some buggy behavior, causing it to be very slow and occasionally fail completely. I wrote this function as a replacement.
The bugs were corrected in R2006b, but I kept this version around because it handled polygon holes more robustly than the original: bufferm simply filled them in, while bufferm2 trims or pads holes according to the buffer width.
Somewhere between R2006b and R2013a, the behavior of bufferm.m was updated to handle holes in the same way as my version. So now, really the only difference between the two is that mine can be applied in cartesian coordinates.
Syntax
[latb,lonb] = bufferm2(lat,lon,dist,direction)
[latb,lonb] = bufferm2(lat,lon,dist,direction,npts)
[latb,lonb] = bufferm2(lat,lon,dist,direction,npts,outputformat)
[xb, yb] = bufferm2('xy',x,y,dist,direction,npts,outputformat)
See function help for description of input and output variables.
Example
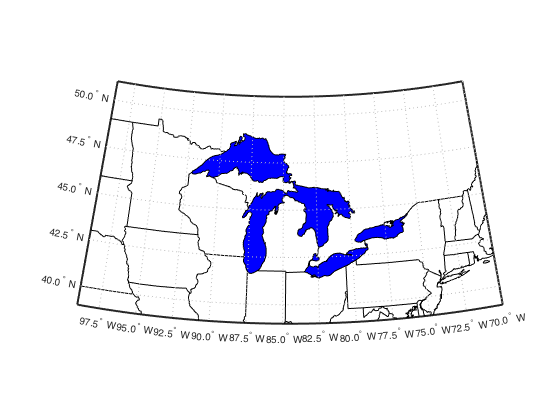
We'll use the Great Lakes polygons as our starting point.
load conus;
usamap({'MN','NY'});
geoshow(uslat, uslon, 'color', 'k');
geoshow(statelat, statelon, 'color', 'k');
geoshow(gtlakelat, gtlakelon,...
'DisplayType', 'polygon', 'FaceColor', 'blue')Calculate a 1-deg outward buffer. We use a reduced-point version of the polygon as our input, since most of the little features will be smoothed out by the buffering process anyway. The result of this calculation is the same as from the bufferm function.
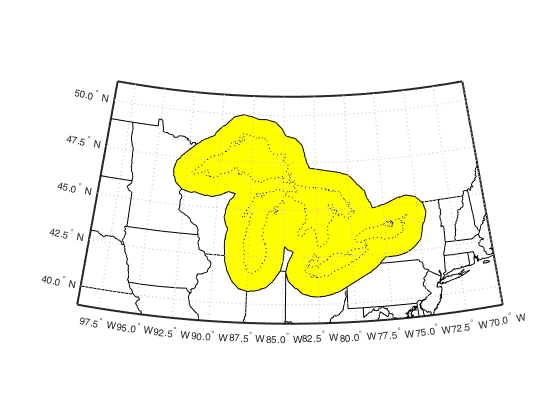
tol = 0.1;
[reducedlat, reducedlon] = reducem(gtlakelat, gtlakelon, tol);
dist = 1;
[latb, lonb] = bufferm2(reducedlat, reducedlon, dist, 'out');
geoshow(latb, lonb, 'DisplayType', 'polygon', 'FaceColor', 'yellow');
geoshow(gtlakelat, gtlakelon, 'color', 'b', 'linestyle', ':');Cite As
Kelly Kearney (2024). bufferm2 (https://github.com/kakearney/bufferm2-pkg), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Mapping Toolbox > Map Display >
- Radar > Mapping Toolbox > Map Display >
- MATLAB > Mathematics > Computational Geometry > Elementary Polygons >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
FEX-function_handle
bufferm2
Versions that use the GitHub default branch cannot be downloaded
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.4.0.1 | linked GitHub readme |
|
|
| 1.4.0.0 | Linked to GitHub repository |
|
|
| 1.3.0.0 | Fixed a bug in input checks so input can be either row or column vectors. Also updates internal plot checks to plot in cartesian coordinates so can be used to check both geographic and x-y input. |
||
| 1.1.0.0 | Added ability to work in cartesian coordinates rather than geographic space; updated description and example on webpage. |
||
| 1.0.0.0 | Added link and comments to this web page regarding the updated version of bufferm. |