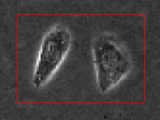
level set for image segmentation
This Matlab code implements a new level set formulation, called distance regularized level set evolution (DRLSE), proposed by Chunming Li et al's in the paper "Distance Regularized Level Set Evolution and its Application to Image Segmentation", IEEE Trans. Image Processing, vol. 19 (12), 2010
The main advantages of DRLSE over conventional level set formulations include the following: 1) it completely eliminates the need for dreinitialization; 2) it allows the use of large time steps to significantly speed up curve evolution, while ensuring numerical accuracy; 3) Very easy to implement and computationally more efficient than conventional level set formulations.
This package only implements an edge-based active contour model as one application of DRLSE. More applications of DRLSE can be found in other published papers in the following website:
Cite As
Chunming Li (2024). level set for image segmentation (https://www.mathworks.com/matlabcentral/fileexchange/12711-level-set-for-image-segmentation), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Image Processing Toolbox > Image Segmentation and Analysis > Image Segmentation >
Tags
Acknowledgements
Inspired: Robust Edge-Stop Functions for Edge-Based Active Contour Models in Medical Image Segmentation, Split Bregman - Globally Convex Segmentation
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
DRLSE_v0/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.9.0.0 | change "VIEW" as "view" in demo1 and demo2 for newer version of Matlab |
||
| 1.6.0.0 | Upgrade the old method to a new one proposed by the same authors in a recently published paper. |
||
| 1.3.0.0 | Added a note about an improvement of this method in the description. |
||
| 1.2.0.0 | This level set method has been improved by Chunming Li in a recent paper, which can be download in his homepage in the following link: |
||
| 1.0.0.0 | update |