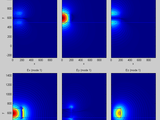
Waveguide Mode Solver
Calculate the electromagnetic eigenmodes and propagation constants of optical waveguides using the finite difference method. Features:
1. Includes vector, semivector, and scalar versions.
2. Can solve for all components of E and H.
3. Allows for perfectly-matched boundary layers.
4. Can model transverse anisotropic materials.
5. Several examples included
Also available at:
http://www.photonics.umd.edu/software/wgmodes/
Published in:
A. B. Fallahkhair, K. S. Li and T. E. Murphy, "Vector Finite Difference Modesolver for Anisotropic Dielectric Waveguides", J. Lightwave Technol. 26(11), 1423-1431, (2008).
Cite As
Thomas Murphy (2024). Waveguide Mode Solver (https://www.mathworks.com/matlabcentral/fileexchange/12734-waveguide-mode-solver), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Image Processing Toolbox > Image Filtering and Enhancement > Image Filtering >
- RF and Mixed Signal > RF Blockset > Equivalent Baseband Simulation >
Tags
Acknowledgements
Inspired: FFT Beam Propagation Method
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
examples/
tools/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.2.0.0 | Corrected bug in stretchmesh routine for south and west boundaries. Also corrected a bug in wgmodes and svmodes in which dy was incorrected conjugated. (Thanks to Jiri Petracek for discovering this bug.) |
||
| 1.1.0.0 | Minor modifications in the examples, and contour plotting subroutine. |
||
| 1.0.0.0 | Corrected an algebraic error in the expressions for the coefficients Axy(E), Axy(W), Axy(N) and Axy(S). Many thanks to yuchunlu_china@hotmail.com for pointing out this bug. |