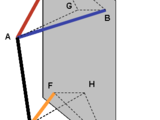
Optimization of a Double Wishbone Suspension System
This demo shows how to use MATLAB, Optimization Toolbox, and Genetic Algorithm and Direct Search Toolbox to optimize the design of a double wishbone suspension system.
Note: You will need to have the following products installed in order to run this demo: MATLAB, Simulink, Optimization Toolbox, Genetic Algorithm and Direct Search Toolbox, and SimMechanics. Optional: Virtual Reality Toolbox.
Cite As
Stuart Kozola (2024). Optimization of a Double Wishbone Suspension System (https://www.mathworks.com/matlabcentral/fileexchange/12837-optimization-of-a-double-wishbone-suspension-system), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Global Optimization Toolbox >
- Simulink > Simulation >
- Physical Modeling > Simscape Multibody > Multibody Modeling >
- Control Systems > Simulink Design Optimization >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.