Kernel Density Estimator
Reliable and extremely fast kernel density estimator for one-dimensional data;
Gaussian kernel is assumed and the bandwidth is chosen automatically;
Unlike many other implementations, this one is immune to problems
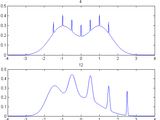
caused by multimodal densities with widely separated modes (see example). The
estimation does not deteriorate for multimodal densities, because we never assume
a parametric model for the data (like those used in rules of thumb).
INPUTS:
data - a vector of data from which the density estimate is constructed;
n - the number of mesh points used in the uniform discretization of the
interval [MIN, MAX]; n has to be a power of two; if n is not a power of two, then
n is rounded up to the next power of two, i.e., n is set to n=2^ceil(log2(n));
the default value of n is n=2^12;
MIN, MAX - defines the interval [MIN,MAX] on which the density estimate is constructed;
the default values of MIN and MAX are:
MIN=min(data)-Range/10 and MAX=max(data)+Range/10, where Range=max(data)-min(data);
OUTPUTS:
bandwidth - the optimal bandwidth (Gaussian kernel assumed);
density - column vector of length 'n' with the values of the density
estimate at the grid points;
xmesh - the grid over which the density estimate is computed;
- If no output is requested, then the code automatically plots a graph of
the density estimate.
cdf - column vector of length 'n' with the values of the cdf
Reference:
Kernel density estimation via diffusion
Z. I. Botev, J. F. Grotowski, and D. P. Kroese (2010)
Annals of Statistics, Volume 38, Number 5, pages 2916-2957
doi:10.1214/10-AOS799
Example (run in command window):
data=[randn(100,1);randn(100,1)*2+35 ;randn(100,1)+55];
kde(data,2^14,min(data)-5,max(data)+5);
Cite As
Zdravko Botev (2024). Kernel Density Estimator (https://www.mathworks.com/matlabcentral/fileexchange/14034-kernel-density-estimator), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired: SimOutUtils, h-coefficient, Kernel Density Estimator for High Dimensions, synctest( X,varargin )
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.5.0.0 | corrected the title back to "kernel density estimator" ; updated reference
|
||
| 1.4.0.0 | -Published in the Annals of Statistics, 2010, see Section 5.
|
||
| 1.3.0.0 | As pointed out by Dazhi Jiang in the comments section, the healine
|
||
| 1.1.0.0 | updated the reference - now a journal paper submitted to the Annals of Statistics |
||
| 1.0.0.0 | Using higher order asymptotic approximations to achieve superior estimation accuracy for problems with few data points. |