FFT Beam Propagation Method
The zip file includes the next programs:
BPM_free_space.m - Propagation of a gaussian pulse in free space
BPM_triangle.m - Propagation of a gaussian pulse in a triangle index profile waveguide
BPM_2step.m - Demonstration of the evanescent waves phenomenon in parallel rectangular waveguides
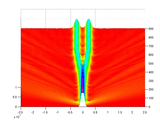
BPM_Y_Branch.m - FFT-BPM in a Y-branch coupler
BPM_mach_zender.m - FFT-BPM simulation of a mach-zender optical switch
REFERENCE:
K. Okamoto, Fundamentals of Optical Waveguides (Academic, 2000).ISBN-13: 978-0125250955
Cite As
Edgar Guevara (2024). FFT Beam Propagation Method (https://www.mathworks.com/matlabcentral/fileexchange/14795-fft-beam-propagation-method), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Mathematics > Fourier Analysis and Filtering >
- Sciences > Physics > Atomic, Molecular & Optical > Optics & Lasers > Optics >
- Sciences > Physics > Accelerators & Beams >
Tags
Acknowledgements
Inspired by: Waveguide Mode Solver, Finite Difference Beam Propagation Method, Finite Differences Beam Propagation Method in 3-D
Inspired: Finite Differences Beam Propagation Method in 3-D, Finite Difference Beam Propagation Method
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.