LMFsolve.m: Levenberg-Marquardt-Fletcher algorithm for nonlinear least squares problems
The function LMFsolve.m serves for finding optimal solution of an overdetermined system of nonlinear equations in the least-squares sense. The standard Levenberg- Marquardt algorithm was modified by Fletcher and coded in FORTRAN many years ago. LMFsolve is its essentially shortened version implemented in MATLAB and complemented by setting iteration parameters as options. This part of the code has been strongly influenced by Duane Hanselman's function mmfsolve.m. Next to it, a finite difference approximation of Jacobian matrix is appended to it as a nested subfunction as well as a function for dispaying of intermediate results.
Calling of the function is rather simple:
[x,ssq,cnt] = LMFsolve(Equations,X0); % or
[x,ssq,cnt] = LMFsolve(Equations,X0,'Name',Value,...); % or
[x,ssq,cnt] = LMFsolve(Equations,X0,Options) % .
In all cases, the applied variables have the following meaning:
* Equations is a function name (string) or a handle defining a set of equations,
* X0 is vector of initial estimates of solutions,
* x is the least-squares solution,
* ssq is sum of squares of equation residuals,
* cnt is a number of iterations
In the first case of call, default values of options are used. The second form of call defines selected options as a set of Name/Value pairs. The last alternative simplifies the statement by introducing earlier defined structure Options of Name\Value pairs.
Field names of the structure options are:
'Display' for control of iteration results,
'MaxIter' for setting maximum number of iterations,
'ScaleD' for defining diagonal matrix of scales,
'FunTol' for tolerance of final function values,
'XTol' for tolerance of final solution increments.
Example:
The general Rosenbrock's function has the form
f(x) = 100(x(2)-x(1)^2)^2 + (1-x(1))^2
Optimum solution gives f(x)=0 for x(1)=x(2)=1. Function f(x) can be expressed in the form
f(x) = f1(x)^2 + f2(x)^2, where f1(x) = 10(x(2)-x(1)^2) and f2(x) = 1-x(1).
Values of the functions f1(x) and f2(x) can be used as residuals.
LMFsolve finds the solution of this problem in 19 iterations. The more complicated problem sounds:
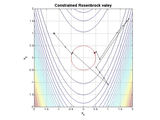
Find the least squares solution of the Rosenbrock valey inside a circle of the unit diameter centered at the origin. It is necessary to build third function, which is zero inside the circle and increasing outside it. This property has, say, the next penalty function:
f3(x) = sqrt(x(1)^2 + x(2)^2) - r, where r is a radius of the circle.
Its implementation using anonymous functions has the form
R = @(x) sqrt(x'*x)-.5; % A distance from the radius r=0.5
ros= @(x) [10*(x(2)-x(1)^2); 1-x(1); (R(x)>0)*R(x)*1000];
[x,ssq,cnt]=LMFsolve(ros,[-1.2,1],'Display',1,'MaxIter',50)
Solution: x = [0.4556; 0.2059], |x| = 0.5000
sum of squares: ssq = 0.2966,
number of iterations: cnt = 51.
Notes:
* Users with old MATLAB versions, which have no anonymous functions implemented, have to call LMFsolve with named function for residuals.
For above example it is
[x,ssq,cnt]=LMFsolve('rosen',[-1.2,1]);
where the function rosen.m is for the given problem of the form
function r = rosen(x)
% Rosenbrock's valey with a constraint R = sqrt(x(2)^2+x(1)^2)-.5;
% Residuals:
r = [10*(x(2)-x(1)^2) % first part
1-x(1) % second part
(R>0)*R*1000 % penalty
];
* The new version of the function LMFsolve is without erroneous part of analytical form of Jacobian matrix.
* The internal function printit.m has been replaced by the function of the same name taken from the more advanced function LMFnlsq (FEX Id 17534) because of much better form of output.
* An error causing an inclination of the previous version to instability has been removed. this step improved stability essentially, however, the a number of iterations increased, if the old version converged at all. However, much better behaviour has the full version of the Fletcher's algorithm, which is implemented in the function LMFnlsq (Id 17534).
* The old (unstable) version of the function is also inclided under the name LMFsolveOLD for those users who liked it.
Reference:
Fletcher, R., (1971): A Modified Marquardt Subroutine for Nonlinear Least Squares. Rpt. AERE-R 6799, Harwell
Cite As
Miroslav Balda (2024). LMFsolve.m: Levenberg-Marquardt-Fletcher algorithm for nonlinear least squares problems (https://www.mathworks.com/matlabcentral/fileexchange/16063-lmfsolve-m-levenberg-marquardt-fletcher-algorithm-for-nonlinear-least-squares-problems), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Optimization Toolbox > Least Squares >
- Mathematics and Optimization > Optimization Toolbox > Systems of Nonlinear Equations >
Tags
Acknowledgements
Inspired by: LMFnlsq - Solution of nonlinear least squares
Inspired: LMFnlsq - Solution of nonlinear least squares, Nlsqbnd
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.3.0.0 | Improved description of the function behavior. Removed bugs in the function LMFsolveOLD names within the code. |
||
| 1.2.0.0 | Removed part of analytical Jacobian matrix causing errors. Removed bug destabilizing the iteration process. Implemented new function for printing intermediate results. |
||
| 1.1.0.0 | Removed erroneous part for analytical form of evaluation of Jacobian matrix. Introduced new function printit.m for better display of iteration results. Removed bug, which cased lower stability of the iteration process. |
||
| 1.0.0.0 | Repaired description, complemented screnshot.
|