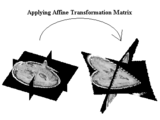
Resampling volume or image with affine matrix
3D Affine matrix is such a 4x4 matrix:
M = [ [R T]; [0 0 0 1] ];
[x2 y2 z2 1]’ = M * [x1 y1 z1 1]’ ;
where, R is a 3x3 rotation matrix, and T is a 3x1 translation matrix. [x1 y1 z1] is a location in original 3D image volume, and [x2 y2 z2] is a location in transformed 3D image volume.
Although affine geometric transformation is only limited to parallel projection, it applies to most of the common geometric transformations, including rotation, translation, scaling, reflection, shearing, etc. Some of the common 3D Affine matrices are listed at the bottom of this description.
It may seem easy if you just want to apply the 3D affine matrix to each [x y z] coordinates in the 3D image volume. However, it turns out to be more complicated when you realize that the voxel (smallest element of 3D image volume) in the transformed image may no longer be an orthogonal cube. Therefore, a 3D interpolation algorithms must also be included to transform 3D image volume. I have implemented three interpolation methods in this program.
Usage: [new_img new_M] = affine(old_img, old_M, [new_elem_size], [verbose], [bg], [method]);
old_img - original 2D image or 3D volume. We assume x for the 1st dimension, y for the 2nd dimension, and z for the 3rd dimension.
old_M - a 3x3 2D affine matrix for 2D image, or a 4x4 3D affine matrix for 3D volume. We assume x for the 1st dimension, y for the 2nd dimension, and z for the 3rd dimension.
new_elem_size (optional) - size of voxel along x y z direction for a transformed 3D volume, or size of pixel along x y for a transformed 2D image. We assume x for the 1st dimension y for the 2nd dimension, and z for the 3rd dimension. 'new_elem_size' is 1 if it is default or empty.
verbose (optional) - 1, 0
1: show transforming progress in percentage
2: progress will not be displayed
'verbose' is 1 if it is default or empty.
bg (optional) - background voxel intensity in any extra corner that is caused by 3D interpolation. 0 in most cases. 'bg' will be the average of two corner voxel intensities in original image volume, if it is default or empty.
method (optional) - 1, 2, or 3
1: for Trilinear interpolation
2: for Nearest Neighbor interpolation
3: for Fischer's Bresenham interpolation
'method' is 1 if it is default or empty.
I suggest that you should use Method 1 (Trilinear) unless you have good reasons to choose other methods. Method 2 (Nearest Neighbor) is slightly faster, but will bring larger interpolation error. The Method 3 (Fischer's Bresenham) is only an implementation to test the special algorithm, and you also need to download my 3D Bresenham's line generation program from:
http://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=21057
new_img - transformed 3D image volume
new_M - transformed affine matrix
This program is inspired by:
SPM5 Software from Wellcome Trust Centre for Neuroimaging
http://www.fil.ion.ucl.ac.uk/spm/software
Fischer, J., A. del Rio (2004). A Fast Method for Applying Rigid Transformations to Volume Data, WSCG2004 Conference.
http://wscg.zcu.cz/wscg2004/Papers_2004_Short/M19.pdf
Although this program (affine3d.m) can also run on MATLAB earlier than version 6.5 (R13), the speed will be hundred times slower. So I suggest that you run this program on MATLAB version 6.5 (R13) and above.
The following script is a demo to show you how to use this program. The result is displayed in the above image.
Example 1 (3D rotation):
load mri.mat; old_img = double(squeeze(D));
old_M = [0.88 0.5 3 -90; -0.5 0.88 3 -126; 0 0 2 -72; 0 0 0 1];
new_img = affine(old_img, old_M, 2);
[x y z] = meshgrid(1:128,1:128,1:27);
sz = size(new_img);
[x1 y1 z1] = meshgrid(1:sz(2),1:sz(1),1:sz(3));
figure; slice(x, y, z, old_img, 64, 64, 13.5);
shading flat; colormap(map); view(-66, 66);
figure; slice(x1, y1, z1, new_img, sz(1)/2, sz(2)/2, sz(3)/2);
shading flat; colormap(map); view(-66, 66);
Example 2 (2D interpolation):
load mri.mat; old_img=D(:,:,1,13)';
old_M = [1 0 0; 0 1 0; 0 0 1];
new_img = affine(old_img, old_M, [.2 .4]);
figure; image(old_img); colormap(map);
figure; image(new_img); colormap(map);
Appendix: Common 3D Affine matrices:
Translation (displacement of [dX dY dZ] for all voxels):
old_M = [
1 0 0 dX
0 1 0 dY
0 0 1 dZ
0 0 0 1 ];
Rotation (about X axis):
old_M = [
1 0 0 0
0 cosX -sinX 0
0 sinX cosX 0
0 0 0 1 ];
Scaling:
old_M = [
sX 0 0 0
0 sY 0 0
0 0 sZ 0
0 0 0 1 ];
Cite As
Jimmy Shen (2024). Resampling volume or image with affine matrix (https://www.mathworks.com/matlabcentral/fileexchange/21080-resampling-volume-or-image-with-affine-matrix), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Image Processing Toolbox > Geometric Transformation and Image Registration >
- Image Processing and Computer Vision > Image Processing Toolbox > 3-D Volumetric Image Processing >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.