probability distribution function (normal distribution)
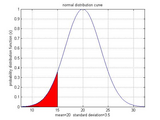
This function calculates the probability under the normal distribution curve, plots the graph and the area calculated.
%Normaldistribution
%
% calculating the area under a normal distribution curve
% from -ve infinity upto point x.
%
% Input:
% x : point on the normal distribution curve
% mean : mean of the normal distribution curve
% sigma : standard deviation of the normal distribution curve
% (hint: normal dist mean=0, sigma=1)
% plotting: Plot the calculated area if plotting = 1
% Output: area under the curve.
%
% Example:
% x=[-20:20] % your data points
% sigma=length(x)/2/3.5 % PDF width is 3.5 sigma
% mean=0 % mean between -20 and 20
% normaldistribution(0, mean, sigma,1) % Calculate area from -inf to 0
%
%
% Author:
% Sherif Omran
% University and university hospital of Zurich
% Date: May 2009
% Part of my phd thesis:
% email: sherif.omran@gmx.de
%-------------------------------------------------------------------------%
Cite As
Sherif Omran (2024). probability distribution function (normal distribution) (https://www.mathworks.com/matlabcentral/fileexchange/23978-probability-distribution-function-normal-distribution), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI, Data Science, and Statistics > Statistics and Machine Learning Toolbox > Probability Distributions >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.