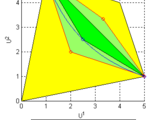
correlated equilibria
by Iskander Karibzhanov
10 Sep 2009
(Updated 18 Mar 2010)
plot set of correlated equilibria and convex hull of Nash equilibria in 2 player normal form game
|
Watch this File
|
| File Information |
| Description |
This program finds efficient/inefficient correlated equilibria that maximize/minimize weighted sum of the payoffs in a two player normal form game
max/min w*U1(P)+(1-w)*U2(P)
s.t. P is correlated equilibrium
where U1 and U2 are given n-by-m matrices of payoffs of two players.
Algorithm builds the linear inequalities that represent the rationality constraints for two players. The constraint matrix A is constructed so that if P is the probability distribution over joint actions, and if X=P(:), the correlated equilibrium constraints are A * X <= 0.
The program also plots the convex hull of found correlated equilibria together with the convex hull of given Nash equilibria which can be solved for by Gambit. http://gambit.sourceforge.net
Author:
Iskander Karibzhanov
PhD student, Department of Economics
University of Minnesota |
| Required Products |
Optimization Toolbox
|
| MATLAB release |
MATLAB 7.9 (2009b)
|
|
Tags for This File
|
| Everyone's Tags |
|
| Tags I've Applied |
|
| Add New Tags |
Please login to tag files.
|
| Updates |
| 23 Sep 2009 |
description updated |
| 18 Mar 2010 |
no arc |
|
Contact us at files@mathworks.com
