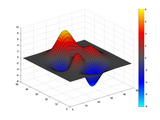
Bipolar Colormap
A symmetric colourmap, with neutral central color, diverging either side to warm colors for positive values, and cold colours for negative ones. This is useful for data where the sign is important, e.g. expansion/contraction in fluid visualisation. This map should allow slightly better distinction of different values within the hot or cold partitions, compared to a map with only two colours (like red-grey-green
The neutral gray-level is user-definable, and the order of the light/dark colors either side automatically switches to match light or dark gray in the centre.
There is also an option to produce a colormap with a linear intensity/luminance variation when results are converted to grayscale. This requires the neutral gray-level to be 0.5.
Cite As
Ged Ridgway (2024). Bipolar Colormap (https://www.mathworks.com/matlabcentral/fileexchange/26026-bipolar-colormap), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Graphics > Formatting and Annotation > Colormaps > Red >
- MATLAB > Graphics > Formatting and Annotation > Colormaps > Blue >
Tags
Acknowledgements
Inspired by: CMRmap.m, mrgb2gray, Tools for NIfTI and ANALYZE image, colorGray, real2rgb & colormaps, Red Blue Colormap
Inspired: squink(Colors,Gamma), jetwhite(Colours)
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.