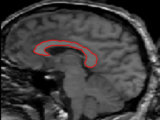
Active Contours: A New Distribution Metric for Image Segmentation
How can we characterize an image, and does the same characterization yield the same result? In this work, we study one possible characterization, distribution metrics. That is, we assume the desired region of interest has a different probability distribution from its corresponding background. Using this, we present a new distribution metric for image segmentation that arises as a result in prediction theory. Forming a natural geodesic, our metric quantifies “distance” for two density functionals as the standard deviation of the difference between logarithms of those distributions. Using level set methods, we incorporate an energy model based on the metric into the Geometric Active Contour framework. We also demonstrate the algorithm on several challenging medical images, which further ensure the viability of the metric in the context of image segmentation.
For More Information: www.romeilsandhu.com/research_projects/p
Cite As
Romeil Sandhu (2024). Active Contours: A New Distribution Metric for Image Segmentation (https://www.mathworks.com/matlabcentral/fileexchange/26101-active-contours-a-new-distribution-metric-for-image-segmentation), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Mapping Toolbox > Geometric Geodesy >
- Radar > Mapping Toolbox > Geometric Geodesy >
- Sciences > Biological and Health Sciences > Biomedical Imaging >
- Image Processing and Computer Vision > Image Processing Toolbox > Image Segmentation and Analysis > Image Segmentation > Active contours >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.