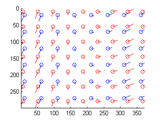
Affine optic flow
An affine (or first-order) optic flow model has 6 parameters, describing image translation, dilation, rotation and shear. The class affine_flow provides methods to estimates these parameters for two frames of an image sequence.
The class implements a least-squares fit of the parameters to estimates of the spatial and temporal grey-level gradients. This is an extension of the well-known Lucas-Kanade method. The images are either sampled conventionally, on a rectilinear grid, or on a log-polar grid. In the latter case, the class may iteratively refine its estimates by moving the sampling grid to track the motion. Options to specify a region of interest and smoothing and sampling parameters are provided.
The file includes a demonstration of the class, and test images for this. The functions for smoothing images and estimating gradients may be useful independently, and log-polar sampling functions are included (and are available separately in submission 27023).
Cite As
David Young (2024). Affine optic flow (https://www.mathworks.com/matlabcentral/fileexchange/27093-affine-optic-flow), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Computer Vision Toolbox > Tracking and Motion Estimation > Motion Estimation >
- Image Processing and Computer Vision > Image Processing Toolbox > Image Filtering and Enhancement > ROI-Based Processing >
- Engineering > Electrical and Computer Engineering > Optics >
Tags
Acknowledgements
Inspired by: Log-polar image sampling, Extended array indexing, Gradients with Gaussian smoothing
Inspired: Muscle fascicle tracking - Ultrasound
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
html/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.3.0.0 | Fixed bug which caused error when sample step was greater than 1. Minor corrections to comments. Changed order of arguments in gsmooth2 and gradients_xyt.
|
||
| 1.2.0.0 | Changed from a function to a class, for more efficient application to image sequences. (Argument checking etc. can be moved outside a loop, and some intermediate computations can be saved for later use.) |
||
| 1.1.0.0 | Fixed bug in use of ROI, allowed ROI in conjunction with log-polar sampling, simplified gradient computation by using exindex, minor changes to demo. |
||
| 1.0.0.0 |