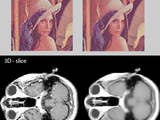
Fast Non-Local Means 1D, 2D Color and 3D
This function NLMF performs Non-Local Means noise filtering of 1D signal, 2D grey/color or 3D image data. The function is partly c-coded for cpu efficient filtering. Suitable for almost every image data type such as MRI, CT and normal photos.
Warning !, Image filtering removes noise, but important (medical) details can also be lost, (see discussion in comments).
Principle NL-Mean filter:
A local pixel region (patch) around a pixel is compared to patches of pixels in the neighbourhood (or in the whole image). The centerpixels of the patches are averaged depending on the quadratic pixel distance between the patches.
Function:
J = NLMF( I, Options);
inputs,
I : 1D signal, 2D grey/color or 3D image data, of type Single or Double in range [0..1]
Options : Struct with options, such as filtering strength
outputs,
J : The NL-means filtered image or image volume
Function(2):
J = NLMF2Dtree(I, Options);
Same as NLMF but will search for the best matches in the whole 2D images using a kd-tree (is still extremely slow)
Literature:
- Non local filter proposed for A. Buades, B. Coll and J.M. Morel "A non-local algorithm for image denoising"
- Basic Matlab implementation of Jose Vicente Manjon-Herrera
Cite As
Dirk-Jan Kroon (2024). Fast Non-Local Means 1D, 2D Color and 3D (https://www.mathworks.com/matlabcentral/fileexchange/27395-fast-non-local-means-1d-2d-color-and-3d), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI, Data Science, and Statistics > Statistics and Machine Learning Toolbox >
- Image Processing and Computer Vision > Image Processing Toolbox > Image Filtering and Enhancement > Image Filtering >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.