Fundamental Matrix Computation
The implemented algorithms are:
1- The normalized 8 point algorithm
2- The algebraic error minimization(iterative)
3- The geometric error minimization(iterative)
and are the algorithms 11.1 to 11.3 of R. Hartley and A. Zisserman "Multiple View Geometry in Computer Vision".
The geometric error minimization includes the gold standard algorithm(MLE) as well as the Sampson approximation to the geometric error.
Usage of the code should be straightforward. The inputs and outputs to the functions, their dimensions and descriptions are available in the headers of each file. try help det_F_normalized_8point for example.
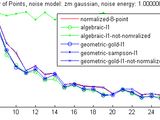
In order to be able to compare the performance of the algorithms, the same criterion as the book: the residual is used(see compare_results.m).
Also, different noise models are utilized to test the robustness of the algorithms: Gaussian additive noise, uniform noise and spurious noise(which can be seen as outliers).
To get the best results, it is possible to initialize the gold standard algorithm with the estimation of F computed from the algebraic minimization algorithm.
Cite As
Omid Aghazadeh (2024). Fundamental Matrix Computation (https://www.mathworks.com/matlabcentral/fileexchange/27541-fundamental-matrix-computation), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |