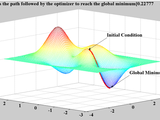
Derivative-based Optimization
This folder contains a word document (optimization_problem_wth_solution.doc) that contains a description for an optimization problem along with its solution. The folder contains two m-script file that contain the solution for the Gradient_Descent_minimum and Gradient_Descent_maximum problems included in the word document. The algorithm for the gradient descent is included in the m-script files. For more information, you could go to wikipedia.
You don't need the optimization toolbox to run the script.
Cite As
Nassim Khaled (2024). Derivative-based Optimization (https://www.mathworks.com/matlabcentral/fileexchange/27631-derivative-based-optimization), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
optimization/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |