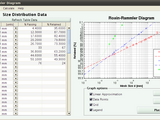
Rosin-Rammler Diagram plotting tool
MATLAB (R) tool for plotting Rosin-Rammler Diagram - a tool with GUI designed for creating Rosin-Ramler Diagrams, calculating Rosin-Rammler distribution parameters and size distribution values based on experimental data. It supports loading and saving experimental size distribution data sets as well as exporting the created graph into all the supported file types.
Rosin-Rammler Diagrams are mainly used to characterize size distribution of various materials.
For more information about algorithms used and RR Diagram itself, see following article:
Improving the effectivity of work with Rosin-Rammler Diagram by using MATLAB(R) GUI tool, Acta Montanistica Slovaca, vol. 15, no. 2, pp. 152-157, 2010
http://actamont.tuke.sk/pdf/2010/n2/7brezani.pdf
Supported by the Scientific Grant Agency (VEGA) of the Ministry of Education of the Slovak Republic and the Slovak Academy of Sciences, Grant No. 1/0752/10.
Cite As
Ivan Brezani (2024). Rosin-Rammler Diagram plotting tool (https://www.mathworks.com/matlabcentral/fileexchange/28013-rosin-rammler-diagram-plotting-tool), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired by: cell2csv, PIVMat 4.20, SETPOS 1.2 - GETPOS 1.2, cell2num, Load Open Document Spreadsheets, csv2cell, dlmcell
Inspired: Rosin-Rammler Diagram plot function
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
RRD - ln/
RRD - ln/funct/
RRD - ln/html/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.16.0.0 | Code simplified. Now using only natural logarithm. Y-TickMarks calculated from Y-Ticks.
|
||
| 1.15.0.0 | Acknowledgement added. |
||
| 1.14.0.0 | Description update |
||
| 1.13.0.0 | In description following link is added: http://actamont.tuke.sk/pdf/2010/n2/7brezani.pdf Onlineavailable article about algorithms used and basic info about RR Diagram (no instructions for using this tool). |
||
| 1.12.0.0 | Updated to version 1.0 (final)
|
||
| 1.11.0.0 | Added option to show % Passing on Y-axis |
||
| 1.9.0.0 | Added copyright and license notes to functions and published html file. |
||
| 1.5.0.0 | Updated to version 0.9 - added support for RR distribution parameters determination by equation fitting (optionally)
|
||
| 1.4.0.0 | Minor changes to html file |
||
| 1.0.0.0 |