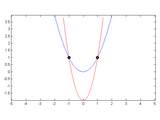
Conics intersection
The homogeneous representation of a conic is a matrix
m = [A C D; C B E; D E F] that represents the equation
A x^2 + B y^2 + 2C xy + 2D x + 2Ey + F = 0
Given two matrix E1 and E2 representing two conics, the code will detect all their intersections.
For instance:
___________________
%a circle centered in the origin
E1 = [1 0 0; 0 1 0; 0 0 -3]
%an ellipse centered in the origin
E2 = [1 0 0; 0 3 0; 0 0 -6]
%get the four homogeneous intersections
P = intersectConics(E1, E2)
%plot the normalized points
plot(P(1,:) ./ P(3,:) , P(2,:) ./ P(3,:), 'ro');
___________________
For more info: http://www.pigei.com/conics-intersection
and a detailed example describing the method: http://math.stackexchange.com/questions/316849/intersection-of-conics-using-matrix-representation
A C++ open souce implementation is also present at https://bitbucket.org/pierluigi/conicsintersection
___________________
If this code was useful, please consider a donation:
Bitcoin: 3BUD7cEnbpp15hZXbPZpdgnH11FAV1kvfi
Cite As
Pierluigi Taddei (2024). Conics intersection (https://www.mathworks.com/matlabcentral/fileexchange/28318-conics-intersection), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.