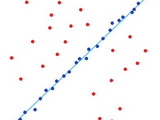
RANSAC algorithm with example of finding homography
Version 1.0.0.0 (5.23 KB) by
Ke Yan
RANSAC algorithm with example of line fitting and finding homography of 2 images
There are 2 implementations of RANdom SAmple Consensus algorithm in the file, one for 2D line fitting only, the other for general purposes(fitting dataA with data B). Example (Finding a homography between 2 images) is provided and the comments are detailed.
Cite As
Ke Yan (2024). RANSAC algorithm with example of finding homography (https://www.mathworks.com/matlabcentral/fileexchange/30809-ransac-algorithm-with-example-of-finding-homography), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Created with
R2010b
Compatible with any release
Platform Compatibility
Windows macOS LinuxCategories
- Image Processing and Computer Vision > Computer Vision Toolbox > Recognition, Object Detection, and Semantic Segmentation > Image Category Classification >
- Image Processing and Computer Vision > Computer Vision Toolbox > Point Cloud Processing > Display Point Clouds >
Find more on Image Category Classification in Help Center and MATLAB Answers
Tags
Acknowledgements
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |