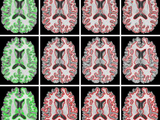
Spatial Fuzzy Clustering and Level Set Segmentation
The performance of the level set segmentation is subject to appropriate initialization and optimal configuration of controlling parameters, which require substantial manual intervention. A new fuzzy level set algorithm is proposed in this paper to facilitate medical image segmentation. It is able to directly evolve from the initial segmentation by spatial fuzzy clustering. The controlling parameters of level set evolution are also estimated from the results of fuzzy clustering. Moreover the fuzzy level set algorithm is enhanced with locally regularized evolution. Such improvements facilitate level set manipulation and lead to more robust segmentation. Performance evaluation of the proposed algorithm was carried on medical images from different modalities. The results confirm its effectiveness for medical image segmentation.
If you think it is helpful, please cite:
----------------------------------------
B.N. Li, C.K. Chui, S.H. Ong, T. Numano, T. Washio, K. Homma, S. Chang, S. Venkatesh, E. Kobayashi (2012) Modeling shear modulus distribution in magnetic resonance elastography with piecewise constant level sets. Magnetic Resonance Imaging 30(3) 390-401.
B.N. Li, C.K. Chui, S. Chang, S.H. Ong (2011) Integrating spatial fuzzy clustering with level set methods for automated medical image segmentation. Computers in Biology and Medicine 41(1) 1-10.
----------------------------------------
Cite As
ABing (2024). Spatial Fuzzy Clustering and Level Set Segmentation (https://www.mathworks.com/matlabcentral/fileexchange/31068-spatial-fuzzy-clustering-and-level-set-segmentation), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired: Selective Level Set Segmentation Using Fuzzy Region Competition
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.