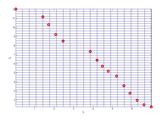
ev-MOGA Multiobjective Evolutionary Algorithm
ev-MOGA Multiobjective Evolutionary Algorithm has been developed by the Predictive Control and Heuristic optimization Group at Universitat Politècnica de València. ev-MOGA is an elitist multi-objective evolutionary algorithm based on the concept of epsilon dominance. ev-MOGA, tries to obtain a good approximation to the Pareto Front in a smart distributed manner with limited memory resources. It also adjusts the limits of the Pareto front dynamically.
Details about ev-MOGA are described in (please, cite this algorithm as):
[1] M. Martínez, J.M. Herrero, J. Sanchis, X. Blasco and S. García-Nieto. Applied Pareto multi-objective optimization by stochastic solvers. Engineering Applications of Artificial Intelligence. Vol. 22 pp. 455 - 465, 2009 (ISSN:0952-1976).
The algorithm is also described in:
[2] J.M. Herrero, M. Martínez, J. Sanchis and X. Blasco. Well-Distributed Pareto Front by Using the epsilon-MOGA Evolutionary Algorithm. Lecture Notes in Computer Science, 4507, pp. 292-299, 2007. Springer-Verlag. (ISSN: 0302-9743)
ev-MOGA has been used in:
[3] J.M. Herrero, X. Blasco, M. Martínez, C. Ramos and J. Sanchis. Robust Identification of a Greenhouse Model using Multi-objective Evolutionary Algorithms. Biosystems Engineering. Vol. 98, Num. 3, pp. 335 - 346, Nov 2007. (ISSN 1537-5110)
[4] J.M. Herrero, X. Blasco , M. Martínez, J. Sanchis. Multiobjective Tuning of Robust PID Controllers Using Evolutionary Algorithms. Lecture Notes in Computer Science, 4974, pp. 515 - 524, 2008. Springer-Verlag. (ISSN: 0302-9743)
[5] J. M. Herrero, S. García-Nieto, X. Blasco, V. Romero-García, J. V. Sánchez-Pérez and L. M. Garcia-Raffi. Optimization of sonic crystal attenuation properties by ev-MOGA multiobjective evolutionary algorithm. Structural and Multidisciplinary Optimization. Vol. 39, num. 2, pp. 203 - 215, 2009 (ISSN:1615-1488).
[6] G. Reynoso, X. Blasco, J. Sanchis. Diseño Multiobjetivo de controladores PID para el Benchmark de Control 2008-2009. Revista Iberoamericana de Automática e Informática Industrial. Vol. 6, Num. 4, pp. 93 - 103 , 2009. (ISSN: 1697-7912)
[7] E. Afzalan, M. Joorabian. Emission, reserve and economic load dispatch problem with non-smooth and non-convex cost functions using epsilon-multi-objective genetic algorithm variable.
Electrical Power and Energy Systems 52 (2013) 55–67
Basic instructions
The “ev-MOGAdescription.pdf” file contains the description of the ev-MOGA algorithm. You should read it before using the algorithm in order to understand how it works. The "ev-MOGA_UserGuide.pdf" file contains a brief description of how to use this toolbox and three illustrative examples.
Cite As
Juan M. Herrero (2024). ev-MOGA Multiobjective Evolutionary Algorithm (https://www.mathworks.com/matlabcentral/fileexchange/31080-ev-moga-multiobjective-evolutionary-algorithm), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Mathematics and Optimization > Global Optimization Toolbox > Multiobjective Optimization >
- Sciences > Agriculture >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
evMOGAtoolbox/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.71.0.0 | bug, in version 1.7, corrected.
|
||
| 1.7.0.0 | Code improvements. Initial population P can be initialized by means of the eMOGA.subpobIni and eMOGA.subpobIni_obj variables. |
||
| 1.6.0.0 | - Bug fixed (anomalous behaviour in first generation when there is only one individual in the pareto front).
|
||
| 1.5.0.0 | Bug fixed |
||
| 1.4.0.0 | The description has been updated |
||
| 1.3.0.0 | Bug fixed and code improvements.
|
||
| 1.2.0.0 | An article which uses evMOGA has been added. |
||
| 1.1.0.0 | ev-MOGA toolbox.pdf file has been modified. |
||
| 1.0.0.0 |