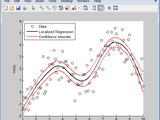
Data Driven Fitting with MATLAB
Data driven fitting allows you to generate a fit without specifying a parametric equation that describes the relationship between your variables.
Fitit.m is a simple function for data driven curve fitting.
FititDemo.m illustrates how to use fitit to generate a curve fit.
Load_Forecasting.m demonstrates building a short term electricity load (or price) forecasting system with MATLAB. Three non-linear regression models (Boosted Decision Trees, Bagged Decision Trees, and Neural Networks) are calibrated to forecast hourly day-ahead loads given temperature forecasts, holiday information and historical loads. The models are trained on hourly data from the NEPOOL region (courtesy ISO New England) from 2004 to 2007 and tested on out-of-sample data from 2008.
Cite As
Richard Willey (2024). Data Driven Fitting with MATLAB (https://www.mathworks.com/matlabcentral/fileexchange/31562-data-driven-fitting-with-matlab), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired: Data Driven Fitting com MATLAB
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.